编译原理一二章
编译原理概述
此部分对应于龙书第一二章
Lec1从代码到可执行文件
编译器要做哪些事情?
一些gcc编译选项
Actions
The action to perform on the input.
-E, --preprocess
Only run the preprocessor
-S, --assemble
Only run preprocess and compilation steps
-c, --compile
Only run preprocess, compile, and assemble steps
-emit-llvm
Use the LLVM representation for assembler and object filesCompilation flags
Flags controlling the behavior of Clang during compilation. These flags have no effect during actions that do not perform compilation.
-Xassembler <arg>`
Pass <arg> to the assembler
-Xclang <arg>, -Xclang=<arg>
Pass <arg> to clang -cc1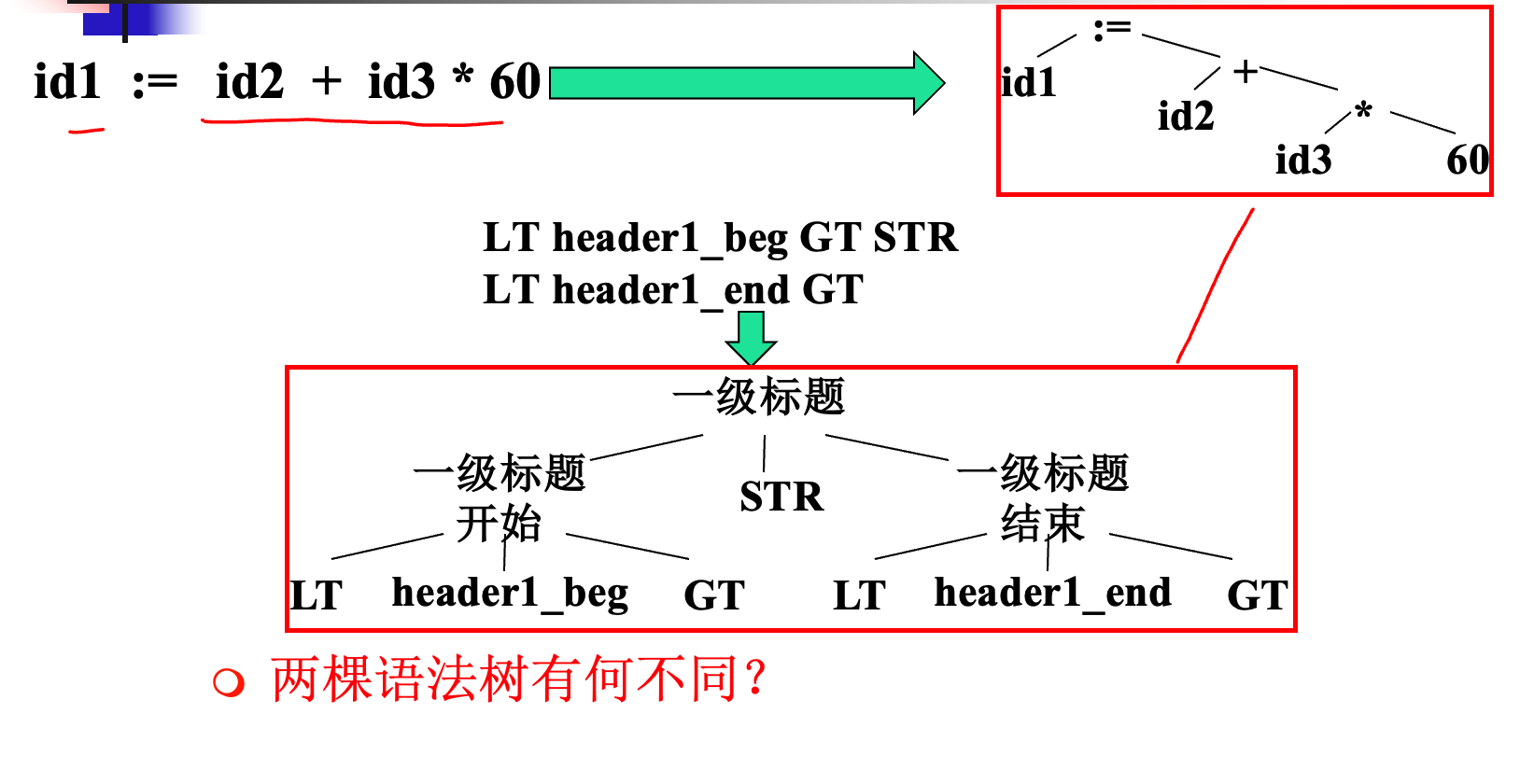
上面是抽象语法树:简化,只包含程序中出现的单词
下面是语义分析树(具体语法树):完整,还包含抽象出的语法概念
对过程的相关理解
C++编译器检查相容类型计算是否合规是在语义分析阶段 编译器识别出标识符是在词法分析阶段
C++编译器过滤注释是在_阶段。 答案是词法分析,但实践表明预处理阶段就已经过滤注释了。 C++编译器检查数组下标越界是在_阶段 C++并不会检查数组下标越界。

显然符号表中不会存变量值,因为变量值在运行时才会确定。
符号表是在词法分析阶段创建的。(习题)
但是据龙书:

Lec2 构造一个简单的编译器
上下文无关文法
感性理解
BNF 是一种 上下文无关文法,那什么是上下文相关文法(CSG呢?
CSG 在 CFG的基础上进一步放宽限制。
产生式的左手边也可以有终结符和非终结符。左手边的终结符就是“上下文”的来源。也就是说匹配的时候不能光看当前匹配到哪里了,还得看当前位置的左右到底有啥(也就是上下文是啥),上下文在这条规则应用的时候并不会被消耗掉,只是“看看”。
形式化定义



对闭包的理解

正闭包也叫正则闭包

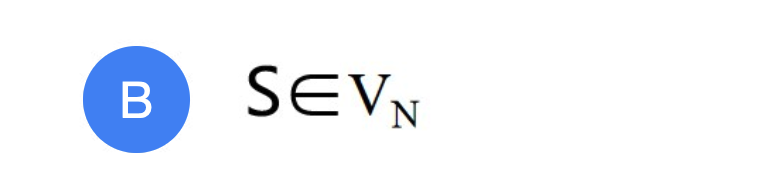

在词法分析阶段,所有的expr都是同等对待的,因此不需要加下标

idlist也可用右递归表示。两种方式等价,但生成的语法分析树不一样。
另外一种设计方案

二义性语法和非二义性语法
非二义性语法
采用二义性语法,则会产生歧义问题,同一段代码在不同编译器上产生不一样的结果,显然是我们不想看到的
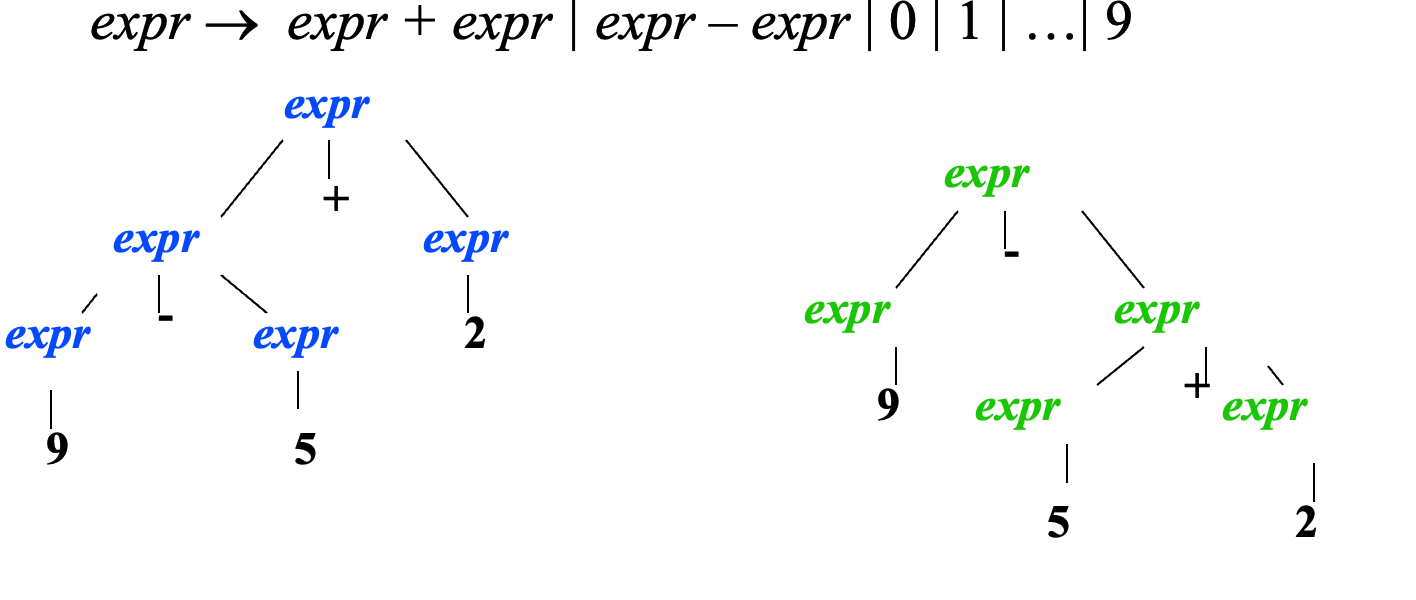
但是在一定的场合下,通过设计合理的语法分析算法,我们是容许一定的二义性的,因为可以减小语法分析树的复杂性。
文法左递归,体现出运算符左结合,右递归则是右结合。
一个右结合的例子
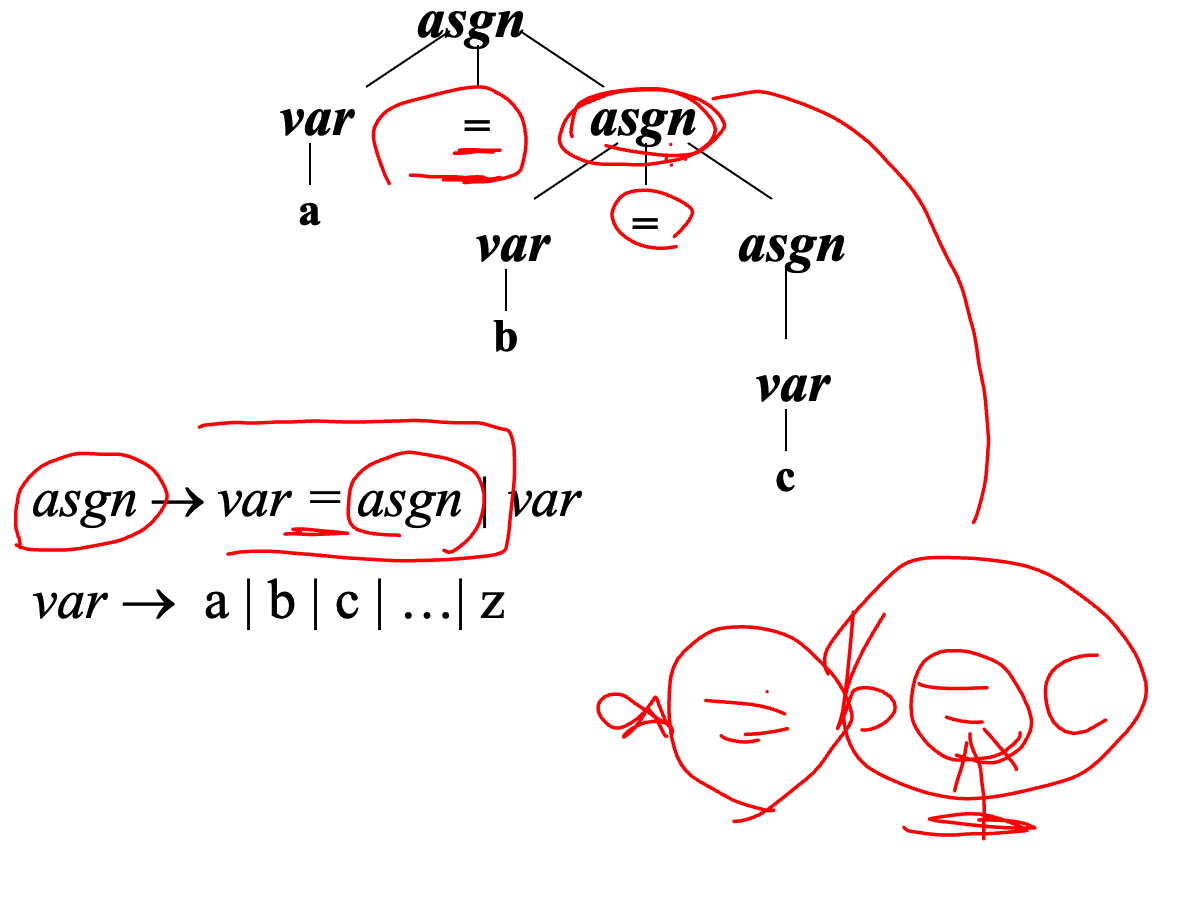

注意:不要跳级!左结合的,且从左往右替换。
练习
推导练习

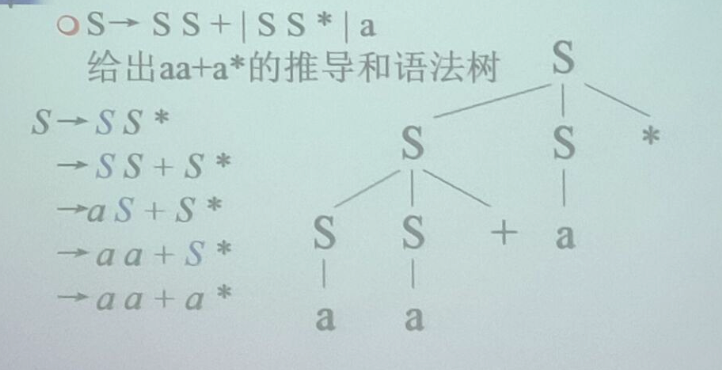

- S -> 0 S 1 | 0 1
- S -> + S S | - S S | a
- S -> S ( S ) S | ε
- S -> a S b S | b S a S | ε
生成的语言:
L = {0n1n | n>=1}
L = {支持加法和减法的表达式的前缀表达形式}
L = {匹配括号的任意排列和嵌套的括号串,包括 ε}
()() (()())等
有二义性:
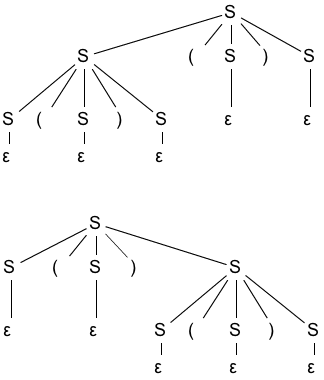
L = {数量相同的a和b组成的符号串,包括 ε}
一个文法有二义性不一定就有两个推导!但一定有两课语法树
构建练习
①
通常左递归对应左结合,右递归对应右结合。
比如对于标识符列表:
- list -> list , id | id
- list -> id , list | id
1是左结合的,2是右结合的。
②
证明:用下面文法生成的所有二进制串的值都能被3整除。`
num -> 11 | 1001 | num 0 | num num
符合该文法的二进制串一定是由任意数量的 11,1001 和 0 组成的最左位不为0的序列
该序列的十进制和为: \[ sum =\Sigma_n\left(2^1+2^0\right) *2^n+\Sigma_m\left(2^3+2^0\right) * 2^m\\ =\Sigma_n 3*2^n+\Sigma_m 9 * 2^m \]
显然是能被3整除的
上面的文法是否能生成所有能被3整除的二进制串?
不能。二进制串10101,数值为21,可被3整除,但无法由文法推导出。
语法制导翻译
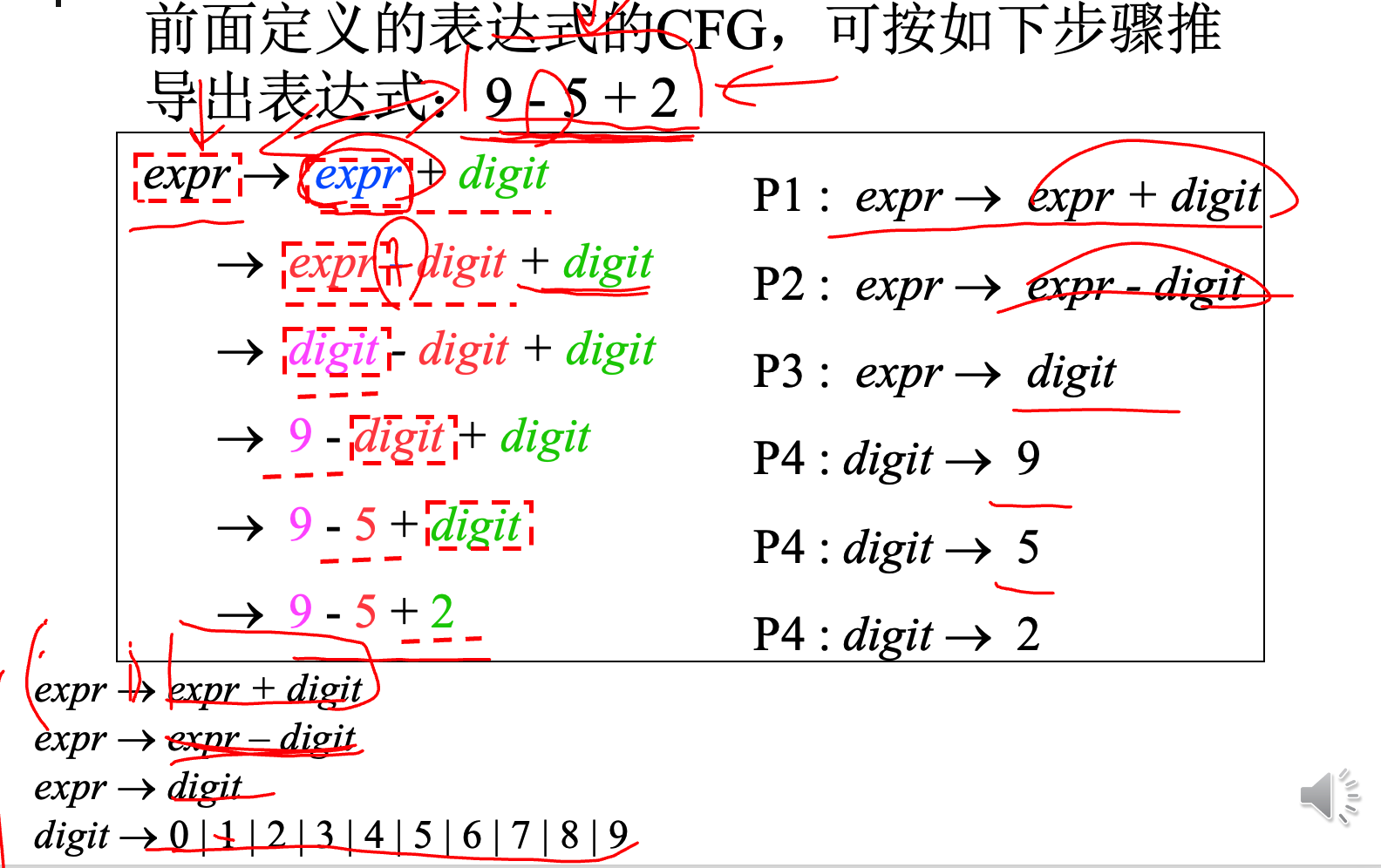
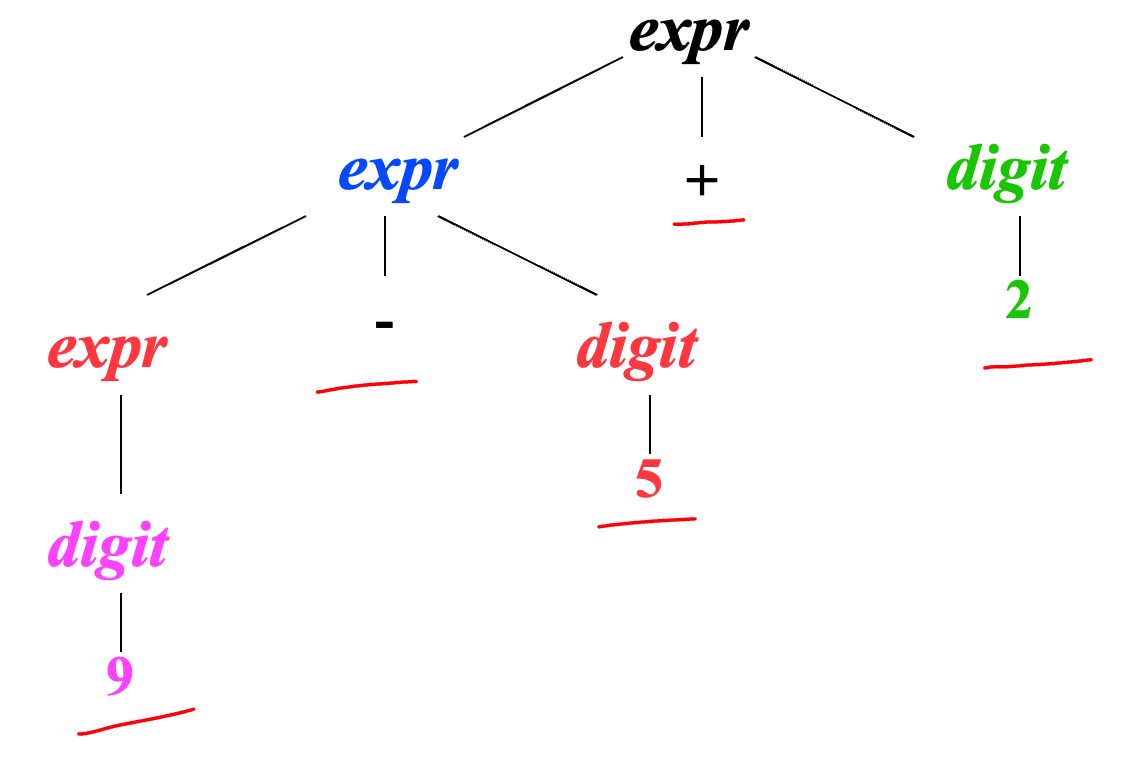
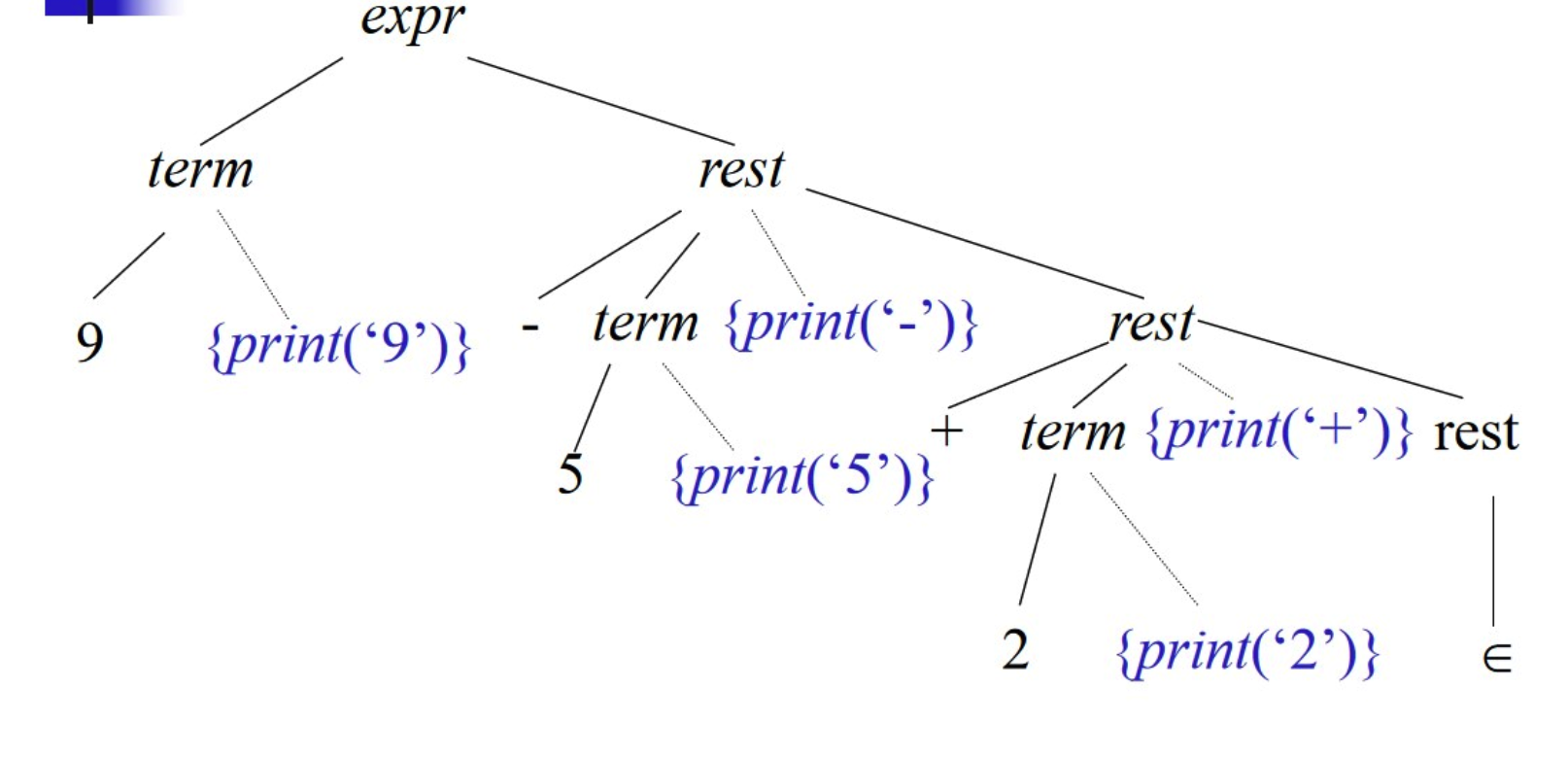
构造翻译模式,中缀->后缀 构造9-5+2的带语义动作的语法分析树,即输出其后缀表达式95-2+
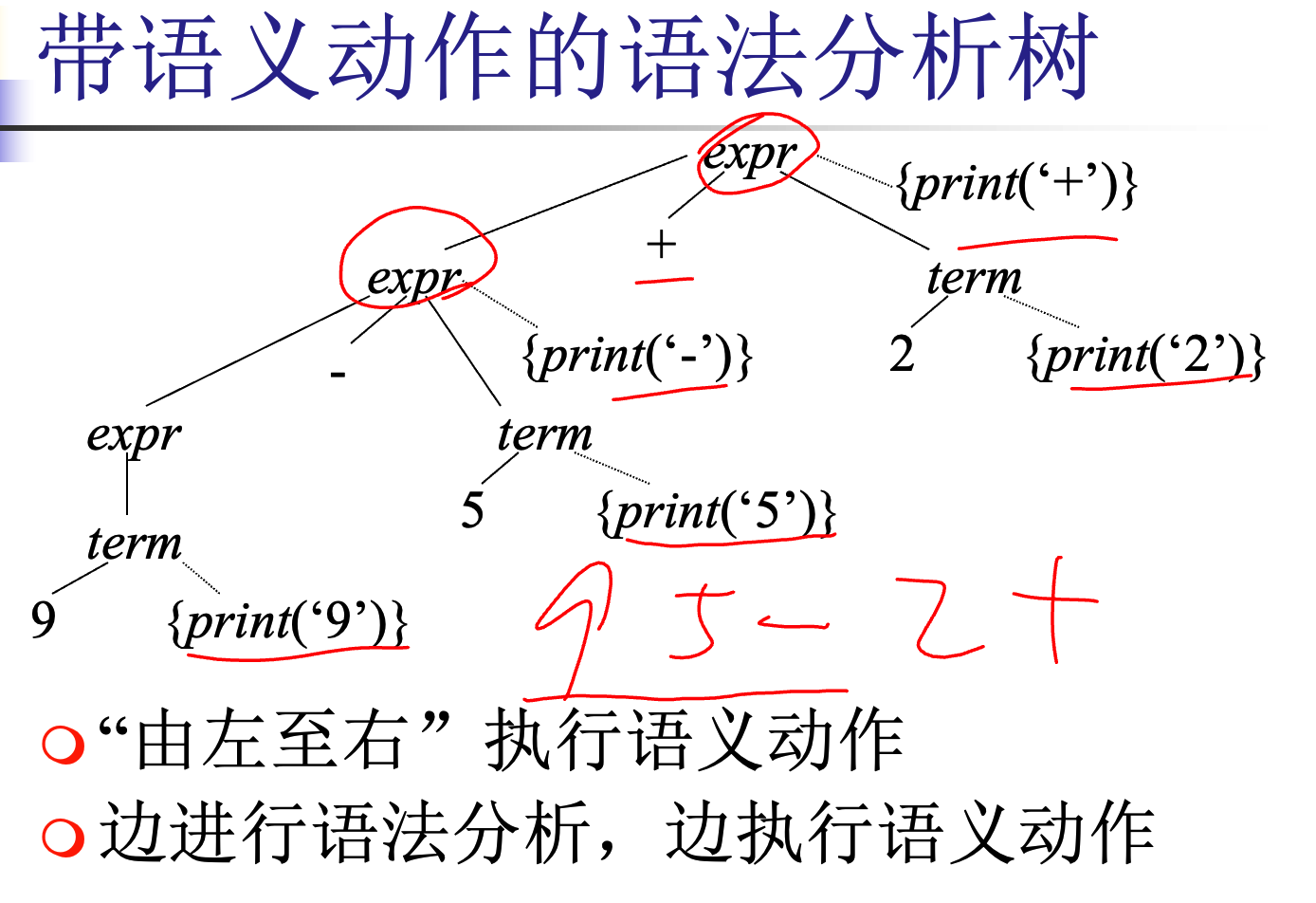
按深度优先遍历即可打印(翻译)出后缀表达式
语法分析
自顶向下构造
平凡算法:扫描输入分析

优化:预测分析

\(lookahead\)在构造编译器的时候就可以完成。
实例分析

对于\(simple\)类似构造方法。
\(lookahead\)怎么构造?

总体思路是什么,还有什么问题?

左递归问题
针对上面的预测分析法,我们发现:左递归会导致递归下降程序无限循环以及预测分析法的失效。
void A(){
switch(lookahead){
case a:
A();match(a);break;
case b:
match(b):break;
default:
report("syntax error")
}
}
怎么消除?
固定的算法:

理解:\(A=\beta \alpha \alpha ...\)
采用右递归进行翻译

练习
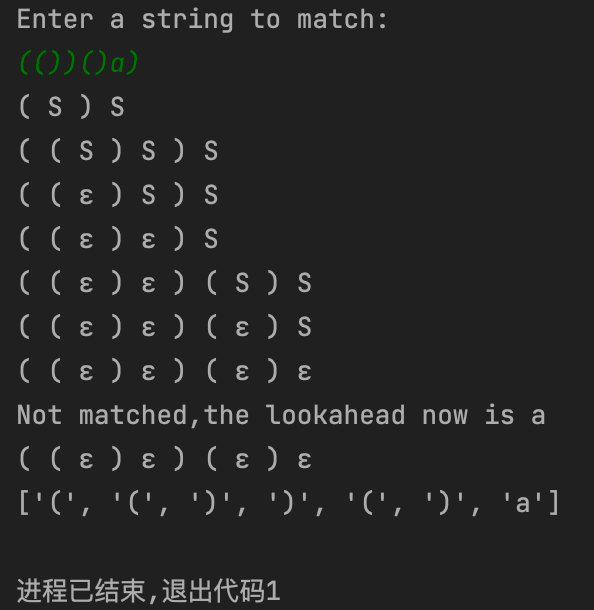
构造 S -> S ( S ) S | ε 的语法分析器
# a program to test lookahead grammar analysis
# S -> S ( S ) S | ε to match brackets
# it can be simplified to S -> ( S ) S | ε
class Matcher:
def __init__(self, string):
self.string = string
self.index = 0
self.lookahead = self.string[self.index] if len(self.string) > 0 else ""
self.process = "S"
self.lookaheads = []
def match(self, char):
if char == '':
return
elif char == self.lookahead:
self.index += 1
if self.index < len(self.string):
self.lookahead = self.string[self.index]
else:
self.lookahead = ""
else:
print("Not matched")
exit(1)
def S(self):
self.lookaheads.append(self.lookahead)
if self.lookahead == '(':
self.process = self.process.replace("S", "( S ) S", 1)
print(self.process)
self.match('(')
self.S()
self.match(')')
self.S()
else:
self.process = self.process.replace("S", "ε", 1)
print(self.process)
self.match('')
def main(self):
self.S()
if self.lookahead == '':
print("Matched")
print(self.process)
print(self.lookaheads)
else:
print("Not matched,the lookahead now is", self.lookahead)
print(self.process)
print(self.lookaheads)
exit(1)
if __name__ == "__main__":
print("Enter a string to match: ")
target = input()
matcher = Matcher(target)
matcher.main()运行结果: