Lenet5 手写数字分类
Lenet5 手写数字分类
2013599 田佳业
实验要求
用Python实现LeNet5来完成对MNIST数据集中10个手写数字的分类。不使用PyTorch或TensorFlow框架。
网络结构
Lenet5的提出在当时主要依靠人工进行特征提取的时代无疑是划时代的。下面阐述原论文中Lenet5得到结构,并同时说明在此次作业中结合当前深度学习发展为加快训练速度和提高准确率做出的改进。
关于维度表示的说明:
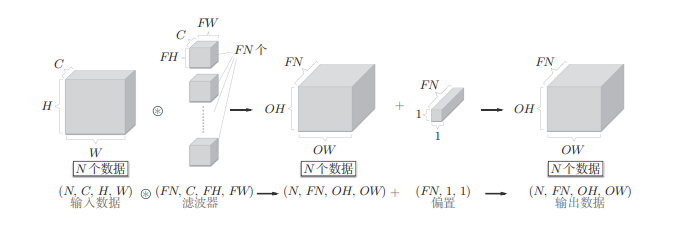
整体的结构图如下所示:
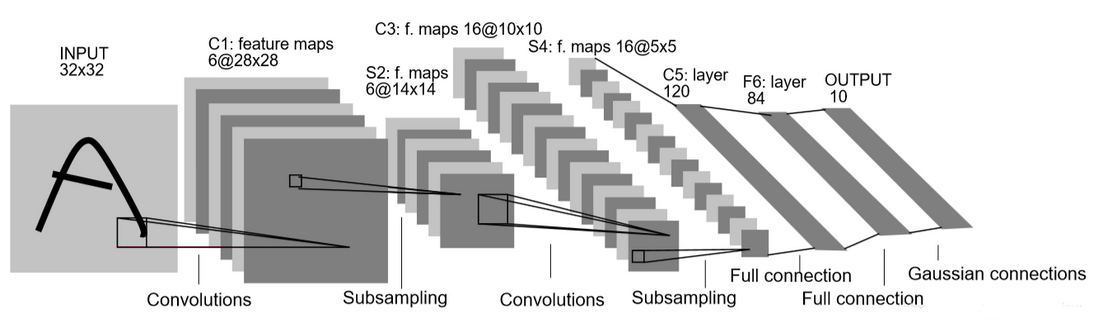
C1 卷积层。
滤波器(6,1,5,5),步长为 1,无 padding,即输入通道数为 1,滤波器数量(等于输出通道数)为 6,大小为5×5 使用偏置项 b。 输出图像大小变为 6 × 28 × 28 。
本次实验中由于图像是28*28的,为尽可能少的改变网络结构,将其进行padding,resize到32*32。
S2 池化层
滤波器 大小 2×2,步长 为2,无 padding,输出矩阵大小为 14×14×6。 > 论文中采用的是平均池化,本次实验中采用最大池化,更能有效的提取关键特征。
C3 卷积层
滤波器 (16,6,5,5),输出图像变为 16 × 5 × 5。
论文中 C3 卷积层的每个滤波器只与上一层中指定的通道进行连接。LeCun认为这样能减少参数数量的同时破坏不同核的对称性,希望不同的核去关注互补的特征。这种策略在现在看来事实上是一种静态的dropout 策略,通常用于缓解过拟合。在Pytorch上实验发现会显著使准确率下降,因此不对其进行实现。
S4 池化层
其设置与 S2 相同。 输出图像大小变为 5 × 5 × 16。
C5-C6 全连接层
其实现与一般的神经网络相同。比如C5图像大小仅为 5 × 5,与滤波器大小相同,因此该层与将输入拉平后进行全连接完全等价。
输出层
论文中采用了欧氏径向基函数(RBF)输出层。RBF 是将计算结果和标准图案进行像素级对比,即预先绘制数字的ASCII点阵图,然后计算输入向量和其欧式距离。这种方法使神经网络的输出有了一定的“可解释性”,但还是局限于特征工程,实现复杂且效果并不比普通的softmax变换好。
激活和损失函数
论文中采用类似于sigmoid的tanh函数作为激活函数,本次实验采用tanh作为激活函数,并在最后使用softmax归一,采用交叉熵误差作为损失函数。
体现在代码中,整个网络的结构定义如下:
class MyLeNet5:
def __init__(self):
self.conv1 = layers.Conv2d(1, 6, 5)
self.relu1 = layers.ReLu()
self.pool1 = layers.MaxPool2d((2, 2))
self.conv2 = layers.Conv2d(6, 16, 5)
self.relu2 = layers.ReLu()
self.pool2 = layers.MaxPool2d((2, 2))
self.fc1 = layers.Linear(16 * 5 * 5, 120)
self.relu3 = layers.ReLu()
self.fc2 = layers.Linear(120, 84)
self.relu4 = layers.ReLu()
self.fc3 = layers.Linear(84, 10)代码细节
准备工作
代码整体仿照Pytorch的形式进行编写,但由于没有Pytorch的自动求导机制,反向传播与参数更新方面必然与其有所差距。
首先进行数据获取和处理,定义模型和优化器:
model = MyLeNet5()
mnist_train = datasets.MNIST('./data/MNIST/raw', train=True)
mnist_test = datasets.MNIST('./data/MNIST/raw', train=False)
mnist_train, mnist_val = split(mnist_train, [54000, 6000])
train_loader = DataLoader(mnist_train, batch_size=120, shuffle=True)
val_loader = DataLoader(mnist_val, batch_size=120, shuffle=False)
test_loader = DataLoader(mnist_test, batch_size=1, shuffle=False)
loss_fn = loss.CrossEntropyLoss()
optimizer = optim.Adam(lr=1e-3)与Pytorch类似,DataLoader实现了迭代器,如下所示:
def __iter__(self):
for i in range(self.num_batches):
batch_indices = self.indices[i * self.batch_size:(i + 1) * self.batch_size]
batch_data = self.data[batch_indices]
batch_labels = self.labels[batch_indices]
yield batch_data, batch_labels交叉熵损失函数如下所示。为避免取对数时数据过小除0,将预测数据过一遍softmax进行归一化:
class CrossEntropyLoss(object):
def __init__(self):
self.input = None
self.output = None
def __call__(self, y_pred, y):
# y_pred: (N, C_out)
# y: (N, 1)
# N = y_pred.shape[0]
# self.input = y_pred
# self.output = np.mean(-np.log(y_pred[range(N), list(y)]))
# grad = y_pred
# grad[range(N), list(y)] -= 1
# grad /= N
# return self.output, grad
N = y_pred.shape[0]
ex = np.exp(y_pred)
sumx = np.sum(ex, axis=1)
loss = np.mean(np.log(sumx)-y_pred[range(N), list(y)])
grad = ex/sumx.reshape(N, 1)
grad[range(N), list(y)] -= 1
grad /= N
return loss, grad优化算法上,论文中使用的是随机梯度下降算法,为加快收敛速度,对当前流行的Adam算法进行了学习和实现。
Adam是2015年提出的新方法。它的理论有些复杂,直观地讲,就是融合了Momentum和AdaGrad的方法,也就是说,结合“速度”和“加速度”进行方向向量判断,同时具有AdaGrad学习率递减的特征。通过组合前面两个方法的优点,有望实现参数空间的高效搜索。此外,进行超参数的“偏置校正”也是Adam的特征。
首先计算历史梯度的一阶指数平滑值,用于得到带有动量的梯度值 \[ m_t=\beta_1^t m_{t-1}+\left(1-\beta_1^t\right) g \] 然后计算历史梯度平方的一阶指数平滑值,用于得到每个权重参数的学习率权重参数 \[ v_t=\beta_2^t v_{t-1}+\left(1-\beta_2^t\right) g^2 \] 对一阶和二阶动量做偏置校正 \[ \begin{aligned} \hat{m}_t & =\frac{m_t}{1-\beta_1^t} \\ \hat{v}_t & =\frac{v_t}{1-\beta_2^t} \end{aligned} \] 最后计算变量更新值,变量更新值正比于历史梯度的一阶指数平滑值,反比于历史梯度平方的一阶指数平滑值 \[ \theta=\theta_{t-1}-\frac{\alpha \hat{m}_t}{\sqrt{\hat{v}_t}+\epsilon} \] Adam会设置 3个超参数。一个是学习率(论文中以α出现),另外两 个是一次momentum系数β1和二次momentum系数\(β2\)。根据论文, 标准的设定值是\(β1\)为 0.9,\(β2\) 为 0.999。
def step(self, params):
vals = params[0]
grads = params[1]
if self.m is None:
self.m, self.v = [], []
for param, grad in zip(vals, grads):
self.m.append(np.zeros_like(param))
self.v.append(np.zeros_like(grad))
self.iter += 1
lr_t = self.lr * np.sqrt(1.0 - self.beta2 ** self.iter) / (1.0 - self.beta1 ** self.iter)
for i in range(len(vals)):
self.m[i] += (1 - self.beta1) * (grads[i] - self.m[i])
self.v[i] += (1 - self.beta2) * (grads[i] ** 2 - self.v[i])
vals[i] -= lr_t * self.m[i] / (np.sqrt(self.v[i]) + 1e-7)
return vals\(\epsilon\)的设置同样是为了防止\(\sqrt{\hat{v}_t}\)过小进行除零运算。代码中将其设为1e-7。
模型实现
layer.py中定义基类layer,各种层均由其继承得来。
卷积层
由于Lenet5中除第一层外不涉及padding和stride不等于1的情况,因此很多地方可以简化实现,加快迭代速度。
其前向传播的运算如下 \[
\mathbf{Y}=\mathbf{x} \otimes \mathbf{W}+\mathbf{b}
\]
我们可以通过im2col来进行优化,将卷积运算转化为矩阵相乘。这篇论文中对im2col实现的排布方式进行了非常直观的展示:
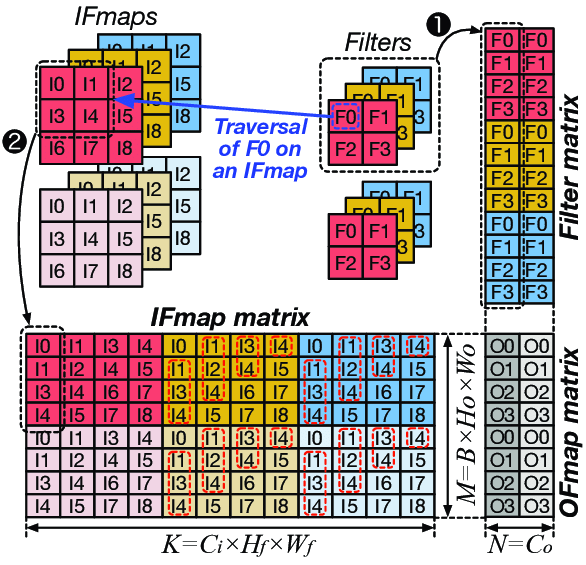
其中\(C_i\)为输入通道个数,图中为3。\(C_o\)为输出通道个数,图中为2。\(H_0\)和\(W_0\)代表卷积后输出图像的高和宽,对应于文中第一张图中的\(OH\)和\(OW\) \[ \begin{aligned} O H & =\frac{H+2 P-F H}{S}+1 \\ O W & =\frac{W+2 P-F W}{S}+1 \end{aligned} \] 本实验中$O H =H-FH+1 \(,\)O W =W-FW+1 $。代码实现可如下:
def im2col(img, filter_h, filter_w, out_H, out_W):
N, C, H, W = img.shape
col = np.zeros((N * out_H * out_W, C * filter_h * filter_w))
for y in range(out_H):
y_start = y * out_W
for x in range(out_W):
col[y_start + x::out_H * out_W, :] = img[:, :, y:y + filter_h, x:x + filter_w].reshape(N, -1)
return col内层循环执行一次,滤波器覆盖的区域被展成“长条”,放到col的对应位置,比如第一次执行内层循环,上图的红黄蓝三条l0 l1 l3 l4均就位。
另外《深度学习入门:基于Python的理论与实现》中有另外一种实现,避免了步长的切片,数据访问局部性更好。
def im2col(img, filter_h, filter_w, out_H, out_W):
N, C, H, W = img.shape
col = np.zeros((N, C, filter_h, filter_w, out_H, out_W))
for h in range(filter_h):
for w in range(filter_w):
col[:, :, h, w, :, :] = img[:, :, h:h + out_H, w:w + out_W]
col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N * out_H * out_W, -1)
return col整个前向传播的实现如下:
def forward(self, X):
N, C, H, W = X.shape
out_H = H - self.filter_size + 1
out_W = W - self.filter_size + 1
# use im2col to convert input to column
col = im2col(X, self.filter_size, self.filter_size, out_H, out_W)
col_W = self.W.reshape(self.out_channels, -1).T
# thus we can use matrix multiplication to calculate output
out = np.dot(col, col_W) + self.b
out = out.reshape(N, out_H, out_W, -1).transpose(0, 3, 1, 2)
self.X = X
self.col = col
self.col_W = col_W
return out对于反向传播,可以通过下面简单的例子进行理解:
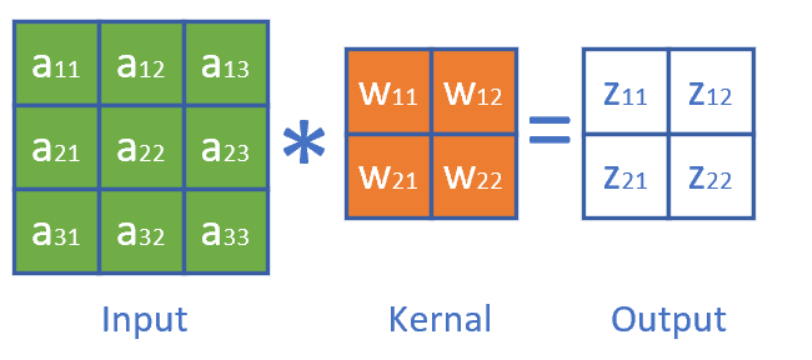
列出 \(a , W , z\) 的矩阵表达式如下: \[ \left[\begin{array}{ll} z_{11} & z_{12} \\ z_{21} & z_{22} \end{array}\right]=\left[\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right] *\left[\begin{array}{cc} w_{11} & w_{12} \\ w_{21} & w_{22} \end{array}\right] \] 利用卷积的定义,很容易得出: \[ \begin{aligned} & z_{11}=a_{11} w_{11}+a_{12} w_{12}+a_{21} w_{21}+a_{22} w_{22} \\ & z_{12}=a_{12} w_{11}+a_{13} w_{12}+a_{22} w_{21}+a_{23} w_{22} \\ & z_{21}=a_{21} w_{11}+a_{22} w_{12}+a_{31} w_{21}+a_{32} w_{22} \\ & z_{22}=a_{22} w_{11}+a_{23} w_{12}+a_{32} w_{21}+a_{33} w_{22} \end{aligned} \]
比如求损失函数 \(J\) 对 \(a_{11}\) 的梯度: \[ \frac{\partial J}{\partial a_{11}}=\frac{\partial J}{\partial z_{11}} \frac{\partial z_{11}}{\partial a_{11}}=\delta_{z 11} \cdot w_{11} \] 上式中, \(\delta_{z 11}\) 是从网络后端回传到本层的 \(z_{11}\) 单元的梯度。 求 \(J\) 对 \(a_{12}\) 的梯度 \(a_{12}\) 对 \(z_{11}\) 和 \(z_{12}\) 都有贡献,二者的偏导数相加: \[ \frac{\partial J}{\partial a_{12}}=\frac{\partial J}{\partial z_{11}} \frac{\partial z_{11}}{\partial a_{12}}+\frac{\partial J}{\partial z_{12}} \frac{\partial z_{12}}{\partial a_{12}}=\delta_{z 11} \cdot w_{12}+\delta_{z 12} \cdot w_{11} \] \[ \frac{\partial J}{\partial a_{22}}=\frac{\partial J}{\partial z_{11}} \frac{\partial z_{11}}{\partial a_{22}}+\frac{\partial J}{\partial z_{12}} \frac{\partial z_{12}}{\partial a_{22}}+\frac{\partial J}{\partial z_{21}} \frac{\partial z_{21}}{\partial a_{22}}+\frac{\partial J}{\partial z_{22}} \frac{\partial z_{22}}{\partial a_{22}} =\delta_{z 11} \cdot w_{22}+\delta_{z 12} \cdot w_{21}+\delta_{z 21} \cdot w_{12}+\delta_{z 22} \cdot w_{11} \] 同理可得所有 \(a\) 的梯度。
观察公式,可以发现把原始的卷积核旋转了180度,再与传入误差项做卷积操作,即可得到所有元素的误差项。
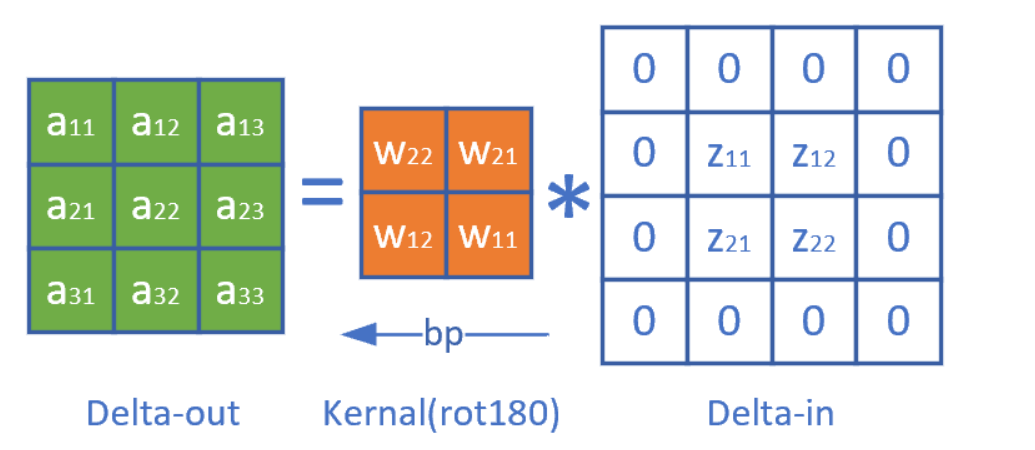
可以得到 \[ \delta_{\text {out }}=\delta_{\text {in }} * W^{\text {rot180 }} \]
同样的道理,对\(\mathbf{W}\)和\(\mathbf{b}\)分别求偏导,可以得到:
\[
\begin{gathered}
\operatorname{\delta}_{\mathbf{W}}=\mathbf{X} \otimes \delta_{\text {in
}} \\
\operatorname{\delta}_{\mathbf{b}}=\sum \delta_{\text {in }}
\end{gathered}
\] 代码中用back_grad指代\(\delta_{\text {in
}}\),表示从后面的层反向传播过来的梯度。
同时结合im2col的逆操作,代码可如下实现:
def backward(self, back_grad):
FN, C, FH, FW = self.W.shape
back_grad = back_grad.transpose(0, 2, 3, 1).reshape(-1, FN)
self.db = np.sum(back_grad, axis=0)
self.dW = np.dot(self.col.T, back_grad)
self.dW = self.dW.transpose(1, 0).reshape(FN, C, FH, FW)
dcol = np.dot(back_grad, self.col_W.T)
dx = col2im(dcol, self.X.shape, FH, FW)
return dx其中col2im作如下实现,道理和im2col类似,不再赘述。
def col2im(col, input_shape, filter_h, filter_w):
N, C, H, W = input_shape
out_H = H - filter_h + 1
out_W = W - filter_w + 1
img = np.zeros((N, C, H, W))
for y in range(out_H):
y_start = y * out_W
for x in range(out_W):
img[:, :, y:y + filter_h, x:x + filter_w] += col[y_start + x::out_H * out_W, :].reshape(N, C, filter_h,
filter_w)
return img池化层
在本次实验中,池化层采用了最大池化的方式,即通过滤波器筛选出最大的元素作为池化结果。反向传播时只有被选择为最大值的元素位置对应会被梯度反向传播,其余的位置都赋值为0。
反向传播也可以通过im2col实现,不过可以利用掩码达到类似的加速效果,且比col2im快。
col2im方法:
def backward(self, back_grad):
back_grad = back_grad.transpose(0, 2, 3, 1)
pool_size = self.pool_H * self.pool_W
dmax = np.zeros((back_grad.size, pool_size))
dmax[np.arange(self.arg_max.size), self.arg_max.flatten()] = back_grad.flatten()
dmax = dmax.reshape(back_grad.shape + (pool_size,))
dcol = dmax.reshape(dmax.shape[0] * dmax.shape[1] * dmax.shape[2], -1)
dx = col2im(dcol, self.X.shape, self.pool_H, self.pool_W)
return dxmask方法:
def backward(self, back_grad):
h_size = self.pool_H
w_size = self.pool_W
N, C, H, W = self.X.shape
output_H = H // h_size
output_W = W // w_size
grad = np.zeros_like(self.X)
for h in range(output_H):
for w in range(output_W):
tmp_x = self.X[:, :, h * h_size:(h + 1) * h_size, w * w_size:(w + 1) * w_size].reshape((N, C, -1))
mask = np.zeros((N, C, h_size * w_size))
mask[np.arange(N)[:, None], np.arange(C)[None, :], np.argmax(tmp_x, axis=2)] = 1
grad[:, :, h * h_size:(h + 1) * h_size, w * w_size:(w + 1) * w_size] = mask.reshape(
(N, C, h_size, w_size)) * back_grad[:, :, h, w][:, :, None, None]
return grad全连接层
全连接层与正常的神经网络基本相同。正向传播就是正常的线性变换,反向传播在实际实现时使用计算图的思想理解比较容易,比如下面是3节点层和2节点层反向传播的示意图:
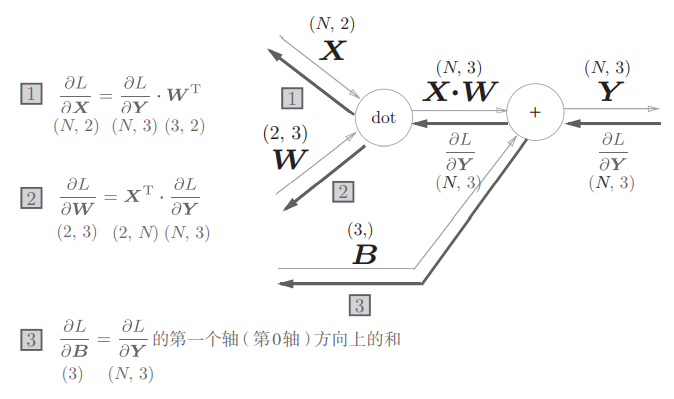
class Linear(Layer):
def __init__(self, input_size, output_size):
super().__init__()
self.input = None
self.output = None
# use "He" initialization
# self.W = np.random.randn(input_size, output_size) * np.sqrt(2 / input_size)
# use normal distribution initialization
self.W = np.random.normal(scale=1e-3, size=(input_size, output_size))
self.b = np.zeros(output_size)
self.dW = np.zeros((input_size, output_size))
self.db = np.zeros(output_size)
def forward(self, X):
self.input = X.copy()
self.output = np.dot(self.input, self.W) + self.b
return self.output
def backward(self, back_grad):
self.dW = np.dot(self.input.T, back_grad)
self.db = np.sum(back_grad, axis=0)
return np.dot(back_grad, self.W.T)实验结果
实验环境
python3.8,依赖numpy及matplotlib。
运行结果及分析
使用54000个数据作为训练集,6000个数据作为验证集,Adam的学习率设置为1e-3。执行20个epoch得到的结果,测试集准确率为98.27%。
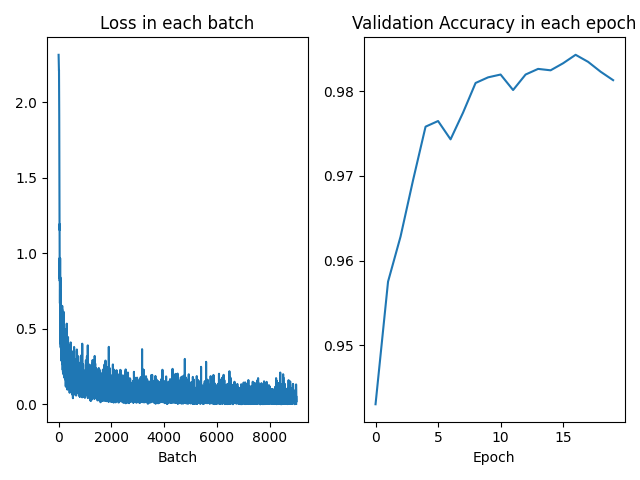
从验证集及损失函数看,模型比较有效的学得了训练集上的参数,且训练集和测试集的正确率同步上升,未发生明显的过拟合。由于并没有对模型进行更细致的参数调优或组合,和LeCun 论文中的 99.27%仍有微小的差距。
同时还打印出了错误分类的样本及其标签,左边为标签,右边为错误预测。可以看到,这些样本很多都比较“奇怪”,即使人来粗看也非常容易犯错。比如右下角的2,本身写的就很难与1分辨开来,一定程度上也说明模型对相似度的正确判断。
