MLP_BP反向传播
MLP_BP反向传播
实验要求
以三层感知机为例,使用反向传播算法更新MLP的权重和偏置项。
Define \(S_w\) and \(S_b\) as: \[ \begin{aligned} &S_w=\sum_{c=1}^C \sum_{\boldsymbol{y}_i^M \in c}\left(\boldsymbol{y}_i^M-\boldsymbol{m}_c^M\right)\left(\boldsymbol{y}_i^M-\boldsymbol{m}_c^M\right)^T \\ &S_b=\sum_{c=1}^C n_c\left(\boldsymbol{m}_c^M-\boldsymbol{m}^M\right)\left(\boldsymbol{m}_c^M-\boldsymbol{m}^M\right)^T \end{aligned} \] where \(m_c^M\) is the mean vector of \(\boldsymbol{y}_i^M\) (the output of the \(i\) th sample from the cth class), \(\boldsymbol{m}^M\) is the mean vector of the output \(\boldsymbol{y}_i^M\) from all classes, \(n_c\) is the number of samples from the cth class. Define the discriminative regularization term \(\operatorname{tr}\left(S_w\right)-\operatorname{tr}\left(S_b\right)\) and incorporate it into the objective function of the MLP: \[ E=\sum_i \sum_j \frac{1}{2}\left(\boldsymbol{y}_{i, j}^M-\boldsymbol{d}_{i, j}\right)^2+\frac{1}{2} \gamma\left(\operatorname{tr}\left(S_w\right)-\operatorname{tr}\left(S_b\right)\right) . \]
符号说明
以经典的手写体识别任务为例,说明本次实验推导所用符号的含义:
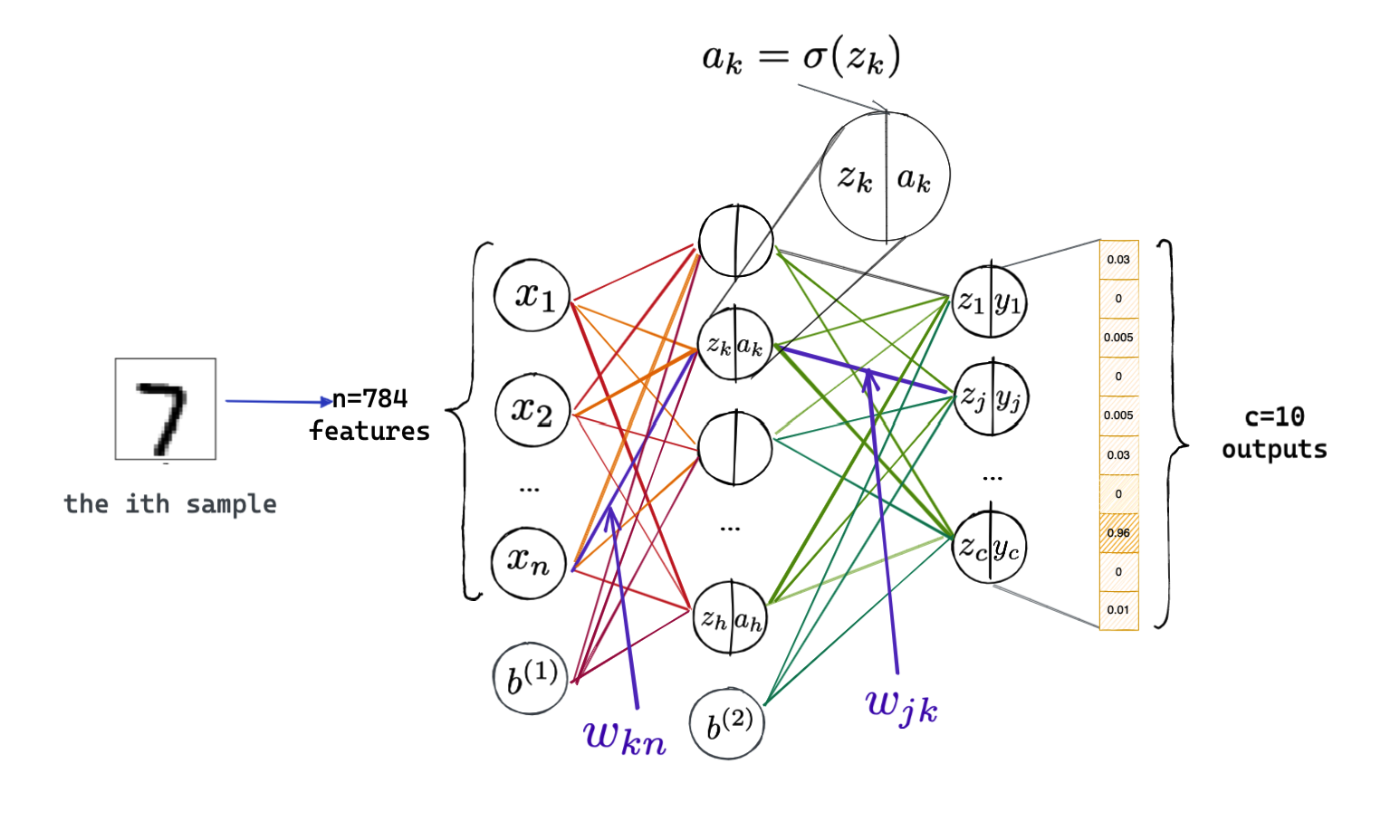
其中\(\sigma\)为激活函数,此处使用sigmoid函数即
\[ \sigma(x)=\frac{1}{1+e^{-x}} \] 导函数为 \[ \sigma^{\prime}(x)=\sigma(x)(1-\sigma(x)) \]
对正则项的理解
首先我们看到,这个题目中的正则项不同于常见的L1正则项或者L2正则项。那么它代表什么含义,又是怎么起到正则化的作用的呢?
在了解了线性判别分析之后,发现这个正则项与线性判别分析中所谓的”类内散度矩阵“和”类问散度矩阵"非常相似。而线性判别分析的核心思想便是”类内方差小、类间间隔大“,在这里也是如此。 \[ \begin{aligned} &S_w=\sum_{c=1}^C \sum_{\boldsymbol{y}_i^M \in c}\left(\boldsymbol{y}_i^M-\boldsymbol{m}_c^M\right)\left(\boldsymbol{y}_i^M-\boldsymbol{m}_c^M\right)^T \\ &S_b=\sum_{c=1}^C n_c\left(\boldsymbol{m}_c^M-\boldsymbol{m}^M\right)\left(\boldsymbol{m}_c^M-\boldsymbol{m}^M\right)^T \end{aligned} \] \[ E=\sum_i \sum_j \frac{1}{2}\left(\boldsymbol{y}_{i, j}^M-\boldsymbol{d}_{i, j}\right)^2+\frac{1}{2} \gamma\left(\operatorname{tr}\left(S_w\right)-\operatorname{tr}\left(S_b\right)\right). \]
从损失函数可以看出,,我们希望让类内散度矩阵\(S_w\)尽可能小,即同一类的样本尽量预测结果一致;同时\(S_b\)是类间散度矩阵,我们希望让它尽可能大,以让模型更好的”区别“开不同的样本。
为了下面分析的方便,对损失函数进行拆解。
容易证明,对于两个阶数都是 \(m \times n\) 的矩阵 \(\boldsymbol{A}_{m \times n}, \boldsymbol{B}_{m \times n}\), 其中一个矩阵乘以 另一个矩阵的转置的迹, 本质是 \(\boldsymbol{A}_{m \times n}, \boldsymbol{B}_{m \times n}\) 两个矩阵对应位置的元素相乘并相加, 可以理解为向量的点积在矩阵上的推广, 即: \[ \begin{aligned} \operatorname{tr}\left(\boldsymbol{A} \boldsymbol{B}^T\right) &=a_{11} b_{11}+a_{12} b_{12}+\cdots+a_{1 n} b_{1 n} \\ &+a_{21} b_{21}+a_{22} b_{22}+\cdots+a_{2 n} b_{2 n} \\ &+\cdots \\ &+a_{m 1} b_{m 1}+a_{m 2} b_{m 2}+\cdots+a_{m n} b_{m n} \end{aligned} \] 则对于题中的列向量也是如此,在损失函数中表现为各元素的平方和。
由此可以得到单个样本单个特征的损失函数: \[ E_{ij}=\frac{1}{2}\left({y}_{i, j}-{d}_{i, j}\right)^2+\frac{1}{2} \gamma\left[\left({y}_{i, j}-{m}_{c,j}\right)^2-\left({m}_{c,j}-m_j\right)^2\right] \]
对此公式符号的含义进行如下直观解释:
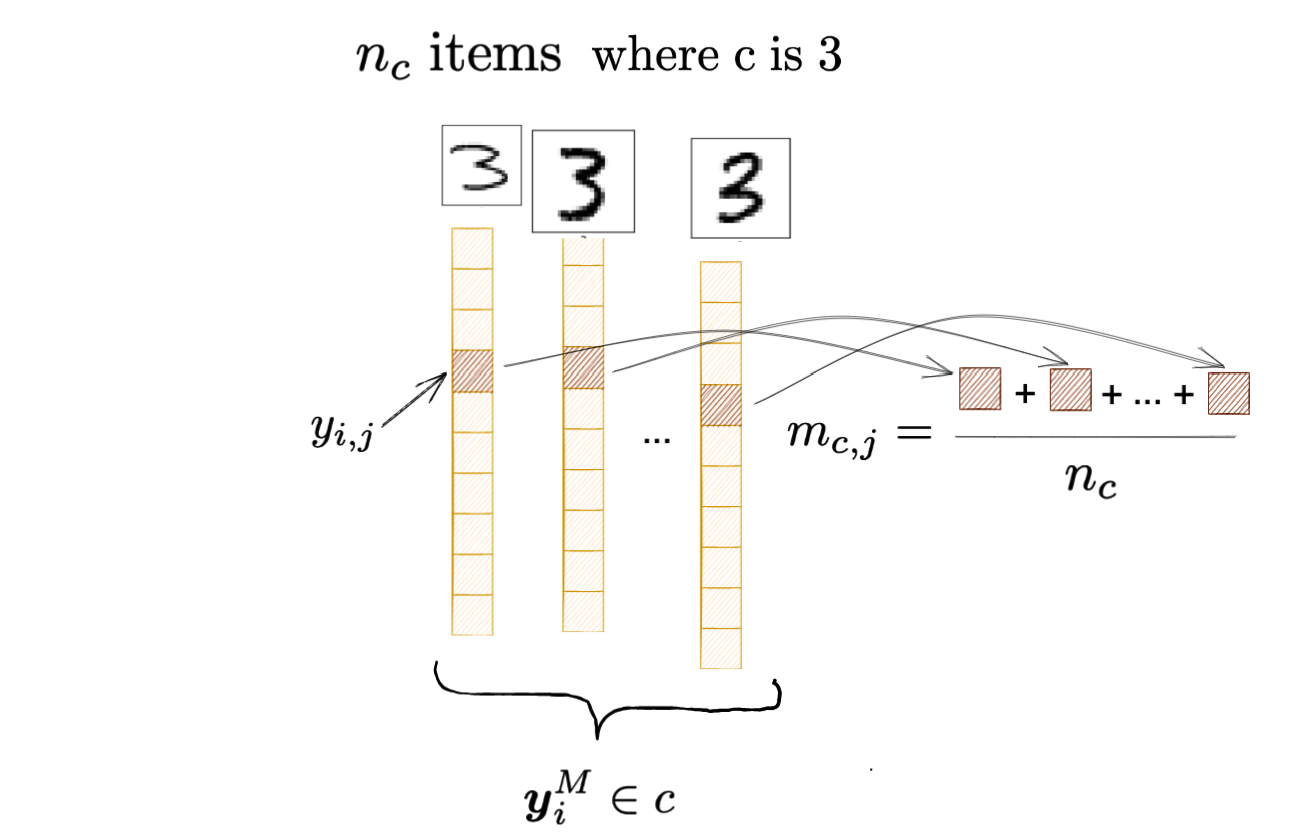
注:上图所指\(j\)也为\(3\);\(m_j\)表示第\(j\)类上的预测值在所有样本上的平均。 ## 梯度下降求解
目标
首先我们需要清楚反向传播的目的:我们希望根据模型在样本上的表现结果调节模型,最小化损失函数以让其在训练集上的表现更好。
具体到神经网络,我们需要调节的是每一条边对应的权重或偏置,依据是损失函数对该层权重的偏导。直观一点说,偏导反映的是参数的微小变化对损失的影响。我们希望最小化损失函数,那么比如如果求出来对权重的偏导是正的,那么说明损失函数随权重增大而增大,那么就要让权重变小一点。
因此我们更新参数的方式如下: \[ \begin{aligned} W^{(l)} &=W^{(l)}-\frac{\alpha}{d }\frac{\partial E}{\partial W^{(l)}}\\ \boldsymbol b^{(l)} &=\boldsymbol b^{(l)}-\frac{\alpha}{d}\frac{\partial E}{\partial b^{(l)}} \end{aligned}\tag{1} \] 其中\(l\)是权重和偏置所在的层数,对于三层感知机\(l=1,2\)。\(\alpha\)为学习率。 \(d\)为整个训练集大小,比如对于MNIST这个值为60000。
偏导求解
在上面定义了对于单个样本单个特征的损失函数。下面为简化叙述,采用逐样本进行偏导的求解。根据题目的含义我们应该是使用批量梯度下降法进行更新,此时将对每个样本求得的偏导加起来求得总的\(E\)代入\((1)\)中(而不是每个样本都使用\((1)\)式进行更新)即可。
也就是 \[ E_i=\sum_{j=1}^{c} E_{ij}\\ E=\sum_{i=1}^{d} E_{i} \]
\(c\)为类的个数,比如手写体识别中为10,数字\(j\)对应于类\(j+1\)。
阅读下面的求解过程时如果担心忘记符号对应的含义,可以将下图固定在屏幕上。

最后一层
从总体来看,对于最后一层的某个边\(w_{jk}\)的权重更新是比较容易进行的。如图所示,\(j=1,2...c\),\(c\)为类别的个数。\(k=1,2...h\),\(h\)为隐层包含的神经元个数。
由链式法则,有:
\[ \frac{\partial E_i}{\partial w_{jk}}= \frac{\partial z_{i,j}}{\partial w_{jk}} \frac{\partial y_{i,j}}{\partial z_{i,j}} \frac{\partial E_i}{\partial y_{i,j}} \] 由于符号定义中第三层的神经元能够比较好的和第二层的区别开,故省略了表示层数的上标;而\(z\)和\(a\)的取值与均与特定的样本有关,故都保留了表示样本的下角标\(i\)。
我们仍旧可以直观的理解链式法则对应于参数更新的含义。我们要求的是损失函数\(E_i\)对\(w_{jk}\)的敏感程度,而\(w_{jk}\)能够直接影响的是\(z_{ij}\),\(z_{i,j}\)影响\(y_{ij}\),\(y_{i,j}\)才直接影响到损失函数。因此需要借助链式法则将这个”影响链“串起来。
\(z_{i,j}\)取决于第二层所有神经元,但我们只需要关注与正在求偏导的边相关的节点: \[ z_{i,j}=\cdots+w_{j k} a_k+\cdots \] 故有 \[ \frac{\partial z_{i,j}}{\partial w_{jk}}=a_{i,k} \] \(y_{i,j}=\sigma\left(z_{ij}\right)\),因此 \(\frac{\partial y_{i,j}}{\partial z_{i,j} }\) 就等于激活函数的导数,即\({\sigma}’\left(z_{i,j}\right)\)。重点是最后一项: \[ \frac{\partial E_i}{\partial y_{i,j}}=\frac{\partial{(\sum_{p=1}^{c} }E_{ip})}{\partial y_{i,j}} \] 而 \[ E_{ip}=\frac{1}{2}\left({y}_{i,p}-{d}_{i, p}\right)^2+\frac{1}{2} \gamma\left[\left({y}_{i, p}-{m}_{c,p}\right)^2-\left({m}_{c,p}-m_p\right)^2\right] \] \(E_{ip}\)中包含\(E_{ij}\),而且我们只关心\(E_{ij}\)。\(E_{ij}\)里面自然有一个\(y_{ij}\)。不仅如此,别忘了\({m}_{c,j}\)和\(m_j\)也都是与\(y_{ij}\)相关的变量,比如 \[ {m}_{c,j}=\frac{1}{n_c}\sum_{N=1}^{n_c}{y}_{N,j} \] \(c_N\)是这个样本所属的类在训练集中的数目,比如这个样本实际上是个"3",那么\(c_N\)就是训练集中"3"的数目。
\({y}_{i, j}\)自然对应\({y}_{N, j}\)中的某一个。因此 \[ \frac{\partial {m}_{c,j}}{\partial y_{ij}}=\frac{1}{n_c} \]
同样的, \[ {m}_{j}=\frac{1}{d}\sum_{N=1}^{d}{y}_{N, j}\\ \frac{\partial {m}_{j}}{\partial y_{ij}}=\frac{1}{d} \] \(d\)是训练集中样本数目。
由此我们可以继续求解:
\[ \begin{align} \frac{\partial E_i}{\partial y_{i,j}}&=\frac{\partial{(\sum_{p=1}^{c} }E_{ip})}{\partial y_{ij}}=\frac{\partial{E_{ij} }}{\partial y_{ij}}\\ &={y}_{i,j}-{d}_{i, j}+\gamma\left[(y_{ij}-m_{c,j})(1-\frac{1}{n_c})-(m_{cj}-m_{j})(\frac{1}{n_c}-\frac{1}{d})\right] \end{align} \]
将上面求得的结果代入对\(w_{jk}\)求偏导的式子中: \[ \begin{align} \frac{\partial E_i}{\partial w_{jk}}&= \frac{\partial z_{i,j}}{\partial w_{jk}} \frac{\partial y_{i,j}}{\partial z_{i,j}} \frac{\partial E_i}{\partial y_{i,j}}\\ &=a_{i,k}\;{\sigma}’\left(z_{i,j}\right)\;\left \{ {y}_{i,j}-{d}_{i, j}+\gamma\left[(y_{ij}-m_{c,j})(1-\frac{1}{n_c})-(m_{cj}-m_{j})(\frac{1}{n_c}-\frac{1}{d})\right]\right \} \end{align} \] 最后,如果我们想要进行批量梯度下降,需要将所有训练集中样本的损失函数加起来求平均,进行一次更新: \[ \begin{align} \frac{\partial E}{\partial w_{jk}}&=\sum_{i=1}^{d} \frac{\partial E_i}{\partial w_{jk}}\\ &=\sum_{i=1}^{d}a_{i,k}\;{\sigma}’\left(z_{i,j}\right)\;\left \{ {y}_{i,j}-{d}_{i, j}+\gamma\left[(y_{ij}-m_{c,j})(1-\frac{1}{n_c})-(m_{cj}-m_{j})(\frac{1}{n_c}-\frac{1}{d})\right]\right \} \end{align} \] 由于三个部分均与\(i\)有关,所以没有可以提取的公因子,需要逐项累加。并且该式子与第\(i\)个样本所属类有关,因此也要根据样本情况代入相应的的\(n_c\)和
\(m_{c,j}\)。
此时我们就可以代入\((1)\)式(更新参数的方式)中,进行每条权重边的更新了。
对于最后一层的\(b_j\)对应偏置的边求解的方式和\(w_{jk}\)类似。 \[ \frac{\partial E_i}{\partial b_{j}}= \frac{\partial z_{i,j}}{\partial b_{j}} \frac{\partial y_{i,j}}{\partial z_{i,j}} \frac{\partial E_i}{\partial y_{i,j}} \] \(\frac{\partial z_{i,j}}{\partial b_{j}}=b^{(2)}\),\(\frac{\partial y_{i,j}}{\partial z_{i,j}}\)和\(\frac{\partial E_i}{\partial y_{i,j}}\)已经求得,代入即可。
倒数第二层
倒数第二层某一条权重边记为\(w_{kn}\)。 \[ \frac{\partial E_i}{\partial w_{kn}}= \frac{\partial z_{i,k}}{\partial w_{kn}} \frac{\partial a_{i,k}}{\partial z_{i,k}} \frac{\partial E_i}{\partial a_{i,k}} \]
重点是\(\frac{\partial E_i}{\partial a_{i,k}}\)。它通过影响最后一层的所有节点去影响最终的损失函数。 \[ \frac{\partial E_i}{\partial a_{i,k}}=\underbrace{\sum_{p=1}^{c} \frac{\partial z_{i,j}}{\partial a_{i,k}} \frac{\partial y_{i,j}}{\partial z_{i,j}} \frac{\partial E_i}{\partial y_{i,j}}}_{\text {Sum over the output layer }} \] 不同于\(z_{i,k}\),\(z_{i,j}\)自然是指最后一层的线性变换。
\(\frac{\partial y_{i,j}}{\partial z_{i,j}} \frac{\partial E_i}{\partial y_{i,j}}\)我们前面已经求得了。\(\frac{\partial z_{i,j}}{\partial a_{i,k}}=w_{jk}\)。
根据递推关系其实也没有很复杂。
前面两项非常容易求得: \[ \frac{\partial a_{i,k}}{\partial z_{i,k}}=\sigma’\left(z_{i,k}\right)\\ \frac{\partial z_{i,k}}{\partial w_{kn}}=x_{i,n} \]
同样的,各个样本上的偏导累加并求平均,然后设置学习率进行梯度下降更新参数即可。 \[ \frac{\partial E_i}{\partial b_{k}}= \frac{\partial z_{i,k}}{\partial b_{k}} \frac{\partial a_{i,k}}{\partial z_{i,k}} \frac{\partial E_i}{\partial a_{i,k}} \] \(\frac{\partial z_{i,k}}{\partial b_{k}}=b^{(1)}\),其余部分也都已经知道了,因此代入即可按同样的方式更新\(\boldsymbol b\)。
至此,所有的权重和偏置项都已经更新完毕。
思考
这个正则项与线性判别分析一样,思路很自然,数学表达也很严谨,确远不如L1或L2正则项用的广泛。虽然并没有基于此做过实验,但从推导的过程可以看到,相比L1或L2正则项直接对权重矩阵的范数求导,计算量明显要大的多。比如至少要预先把预测每一类对应的样本数和样本向量均值算出来,在求偏导时也要判断是属于哪一类,对性能肯定是有所损耗。