人工智能导论
人工智能导论
逻辑推理



任意对析取,存在对合取都是蕴含关系,分开的条件强于合起来的(举个例子就明白了)


只与新加入的直接相关
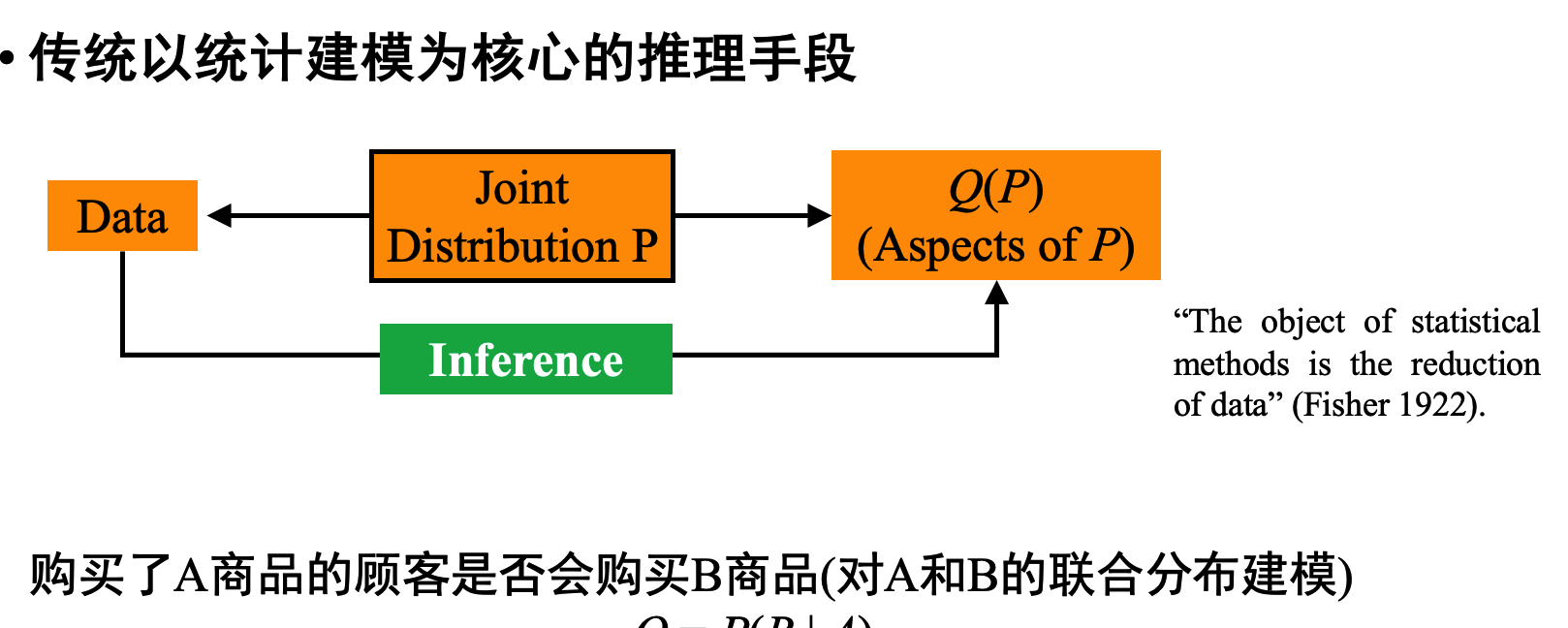


因果分析三层次:关联,介入,反事实
因果图三种形式:链,分连,汇连(chain,fork,collider)
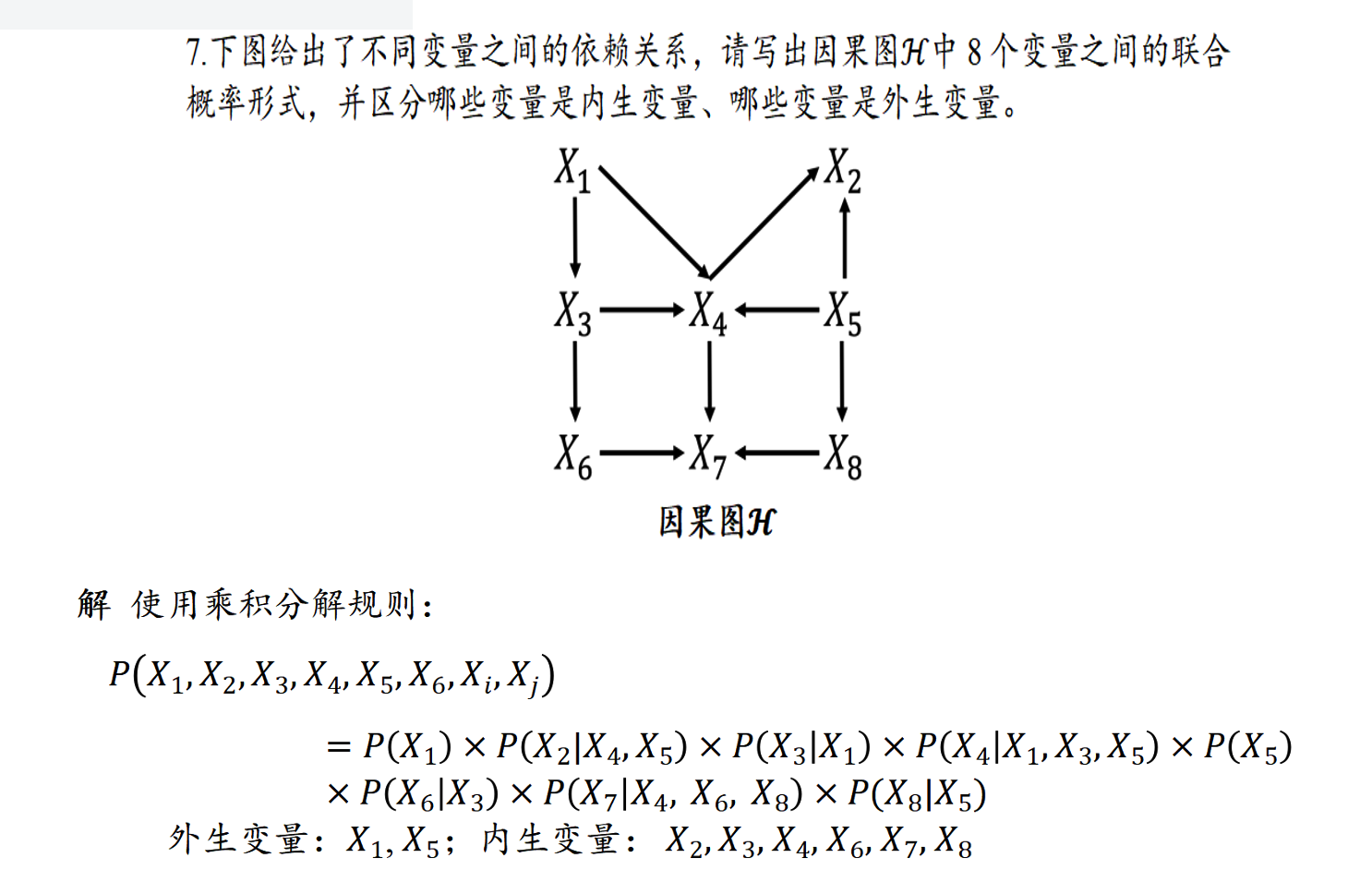
做法:联合概率分布由每个节点与其父节点之间的条件概率得出。根节点是外生变量,其他的是内生

深搜可能会陷入无限循环



有环路的图会使贪婪最佳优先算法不完备。
判断:启发函数满足可容性则一定能保证算法最优性x
树搜索是这样法,图不一定
判断:启发函数恒为0一定满足可容性x
启发函数不一定要是正数。
满足一致性可保证A*搜索算法最优
启发函数不会过高估计从当前节点到目标结点之间的实际代价。x
满足可容性的启发函数才有这样的性质。
MinMax的适用条件:两人博弈,信息透明,零和博弈
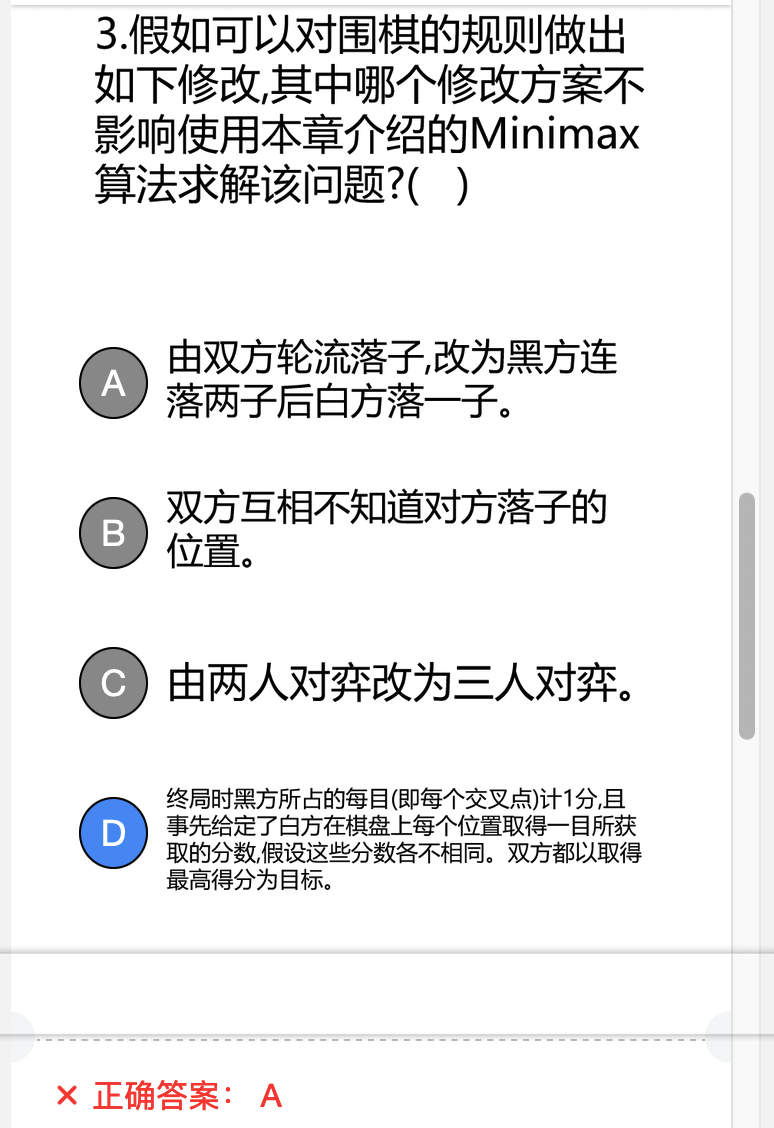
注意,没有规定必须要公平。D违反了零和博弈
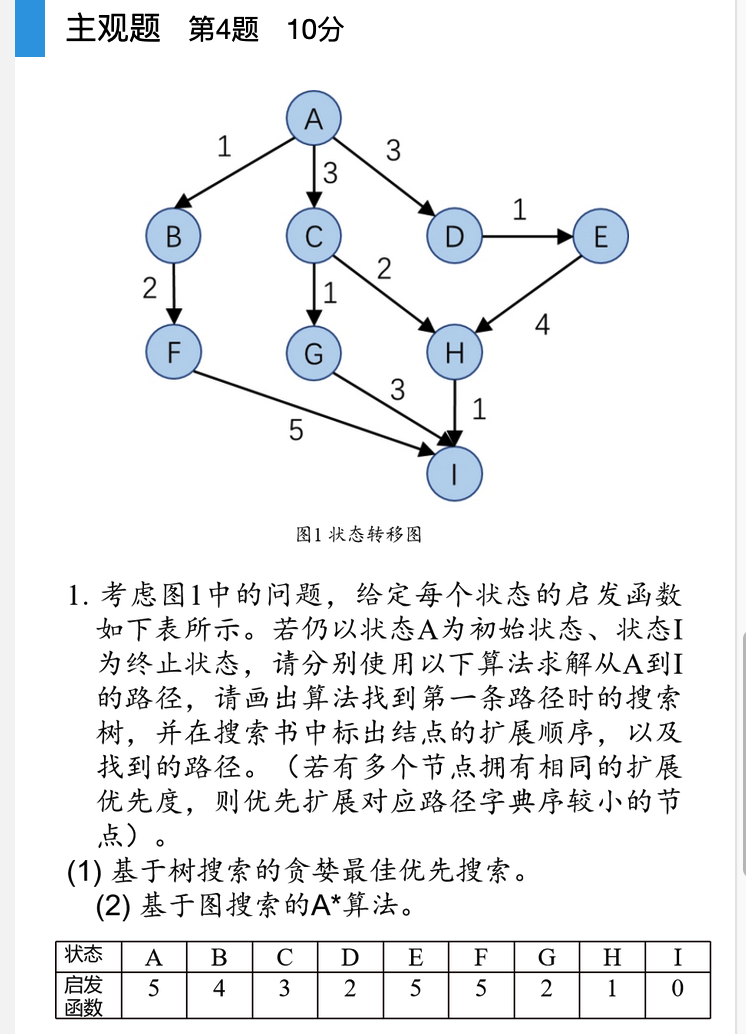
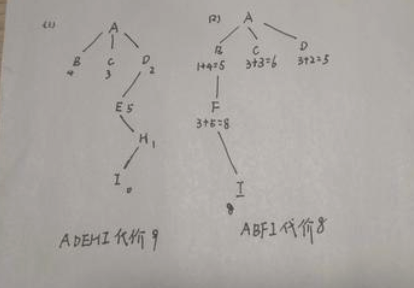
这个做法是不对的,根据课本上的过程,A*算法会考虑所有可达的评价函数,每次从边缘集合拓展的节点并非总是当前节点的后继节点。fn评价函数是唯一标准如果发现有更小的,会倒回去。
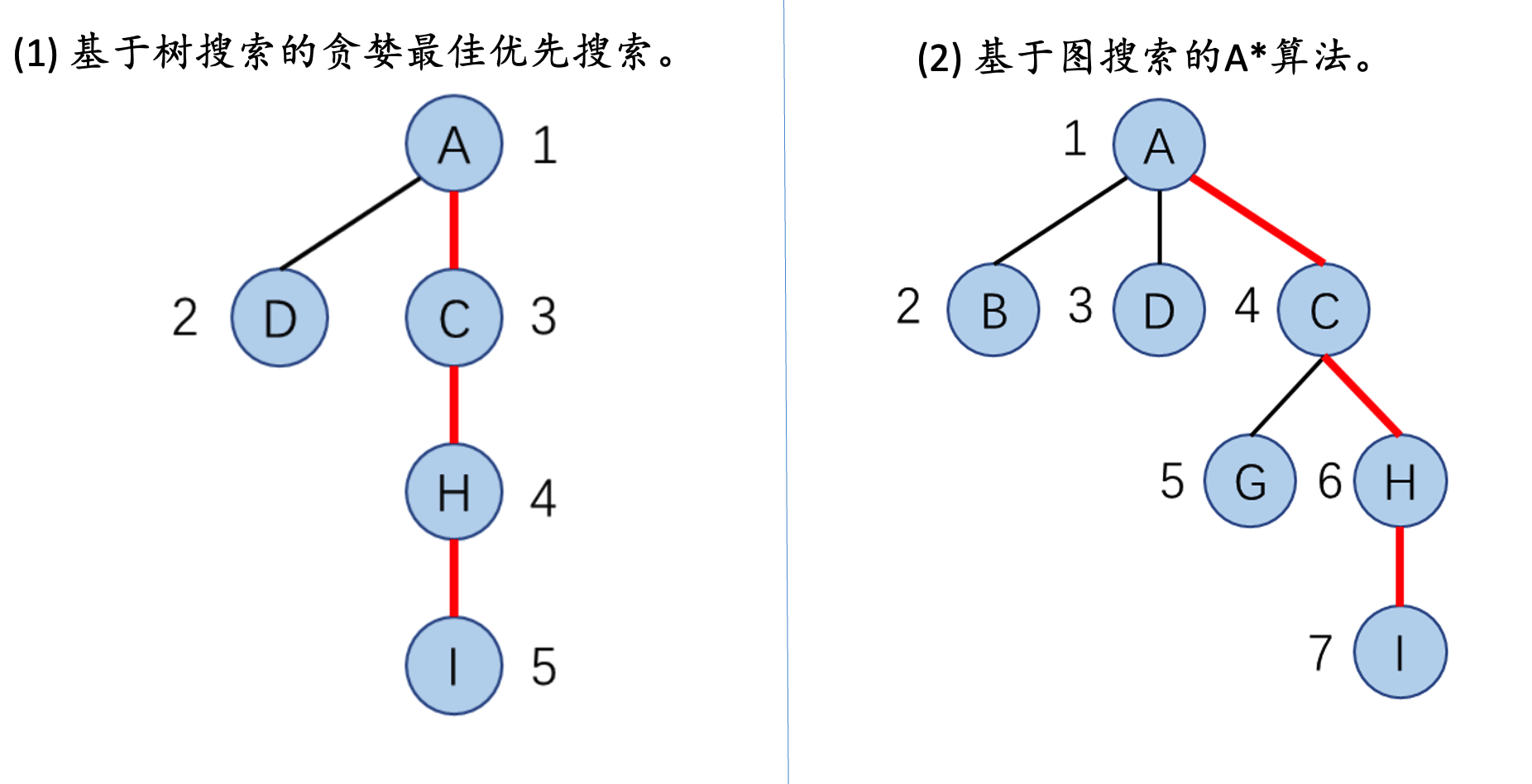
而且贪婪最佳优先搜索也是启发式算法,优先选择启发函数最小的后继节点拓展。


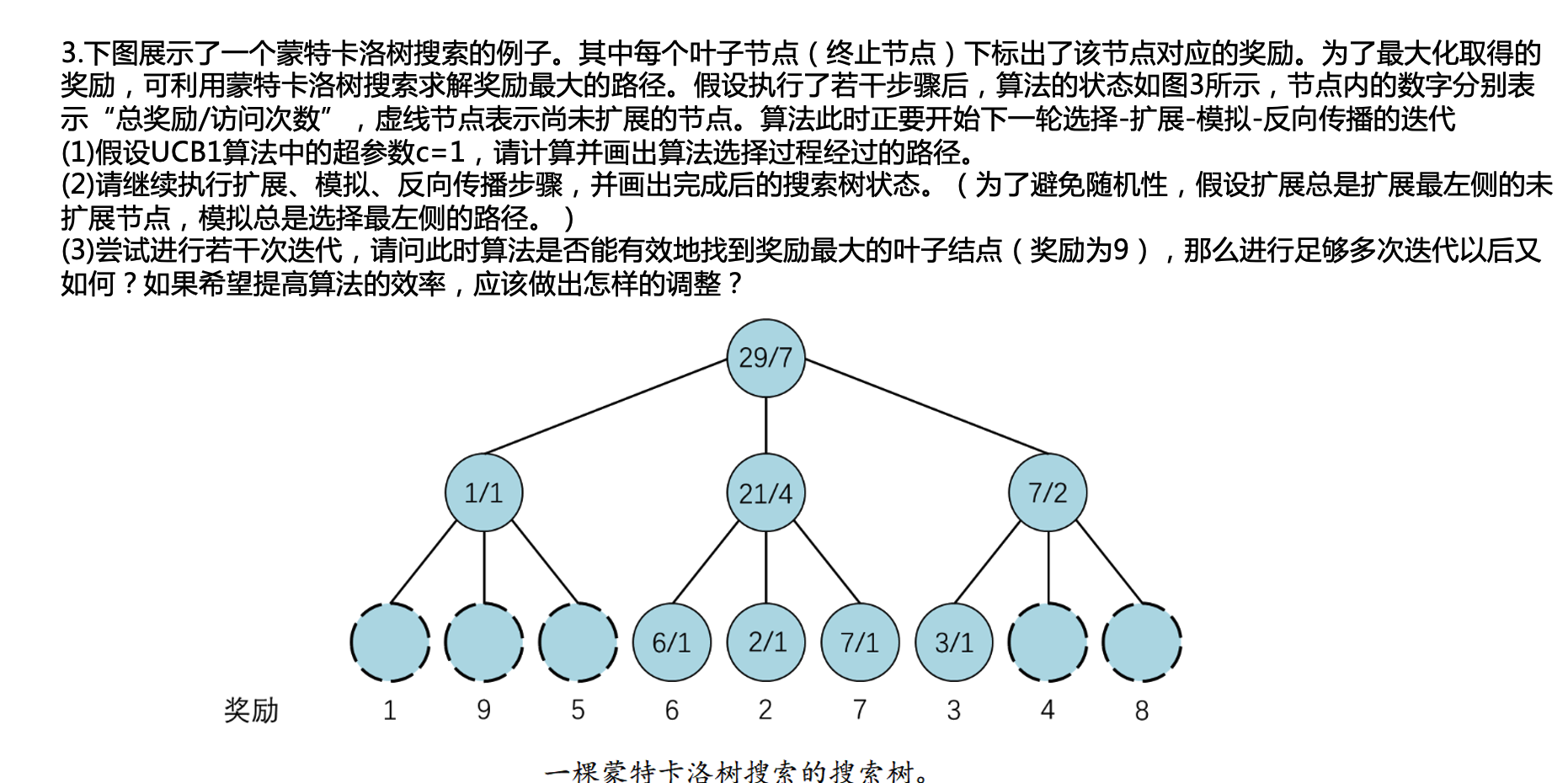
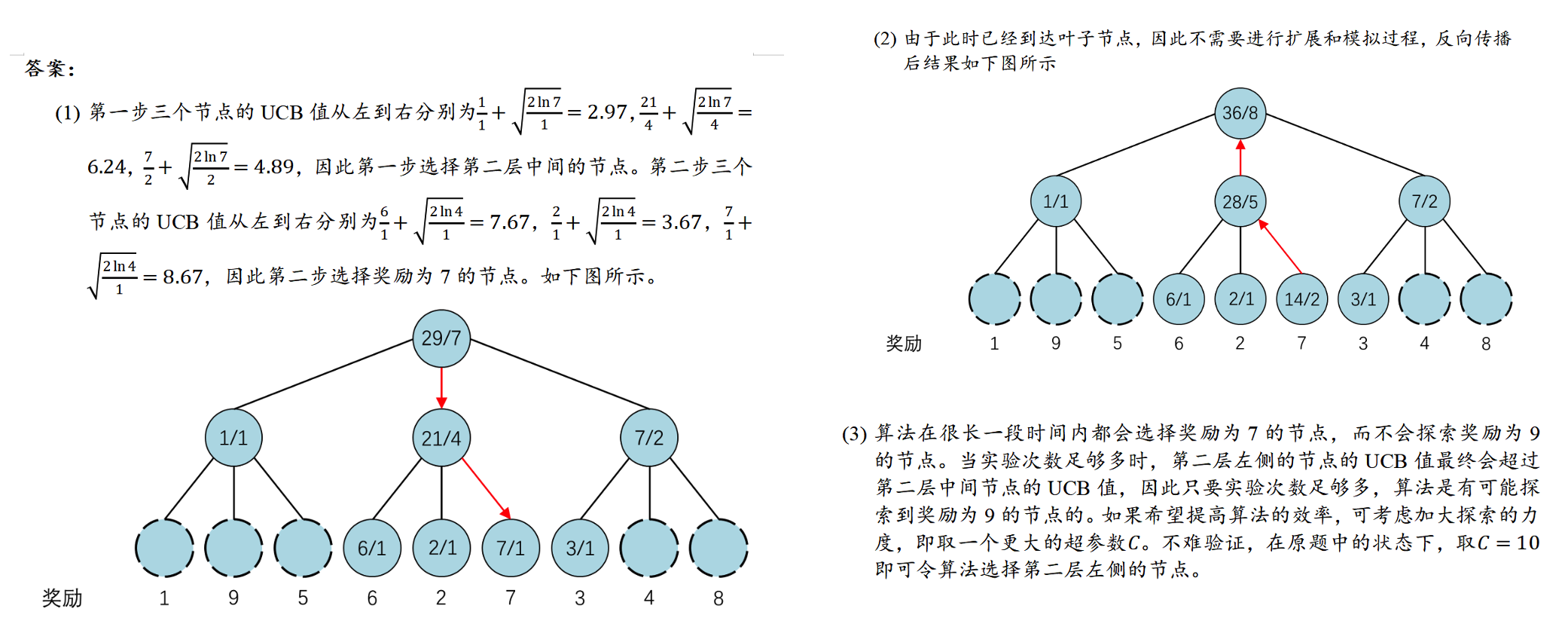
记住蒙特卡洛树UCB的公式,明白反向传播的过程。 \[ U C B=\bar{X}_j+C \times \sqrt{\frac{2 \ln n}{n_j}} \] 上限置信区间 (Upper Confidence Bound, UCB)
监督学习中经验风险和期望风险的概念

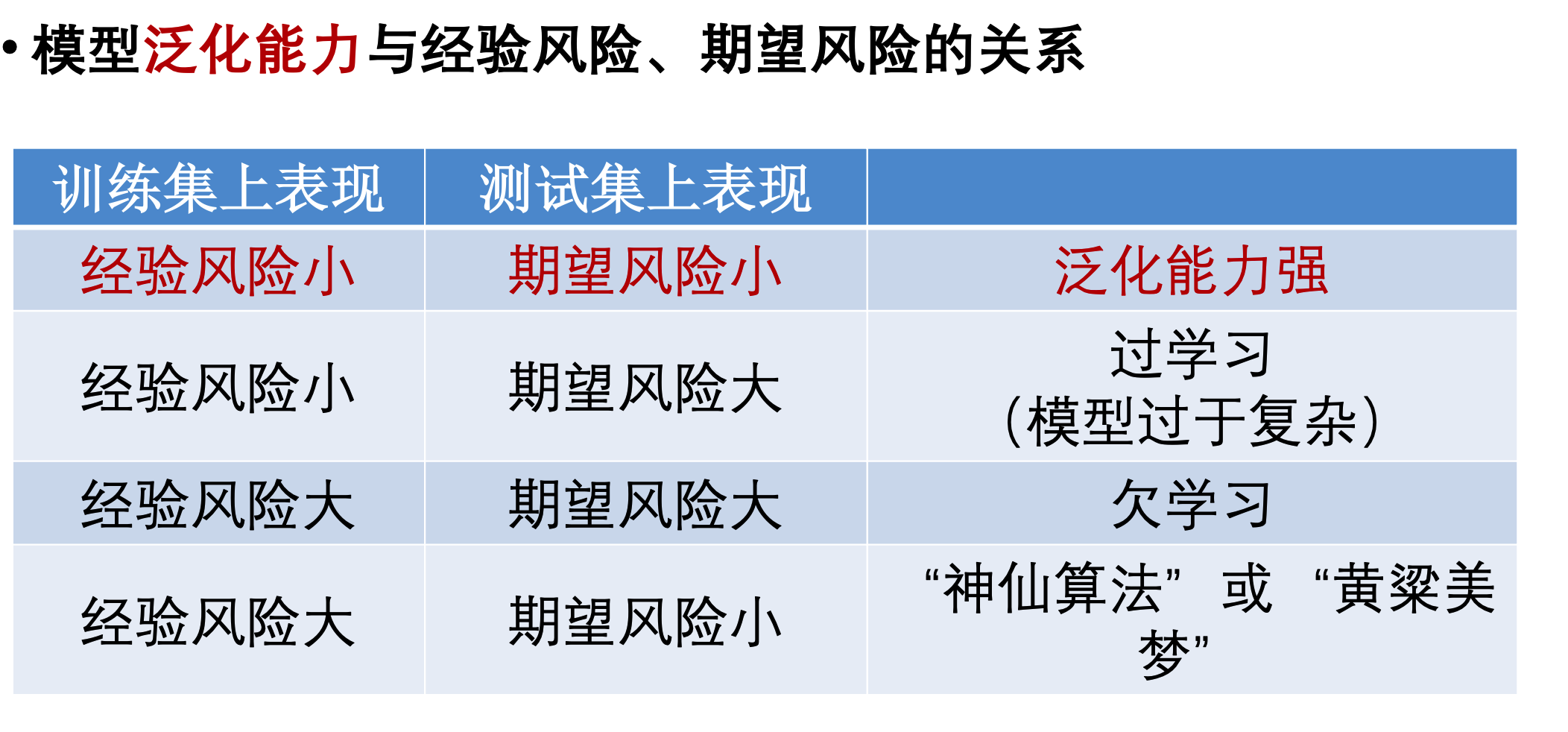


常用的正则项方法包括L1正则项和L2正则项:其中L1使权重稀疏,L2使权重平滑。一句话总结就是:L1会趋向于产生少量的特征,而其他的特征都是0,而L2会选择更多的特征,这些特征都会接近于0。
怎么记:1比2小,生成的特征少


考法:判断哪些算法是判别模型,哪些是生成模型。大部分典型机器学习算法都是判别模型。贝叶斯方法,隐马科代夫链式生成模型

信息熵小,信息稳定,单一,纯度高;信息熵大,信息不稳定,纯度低。
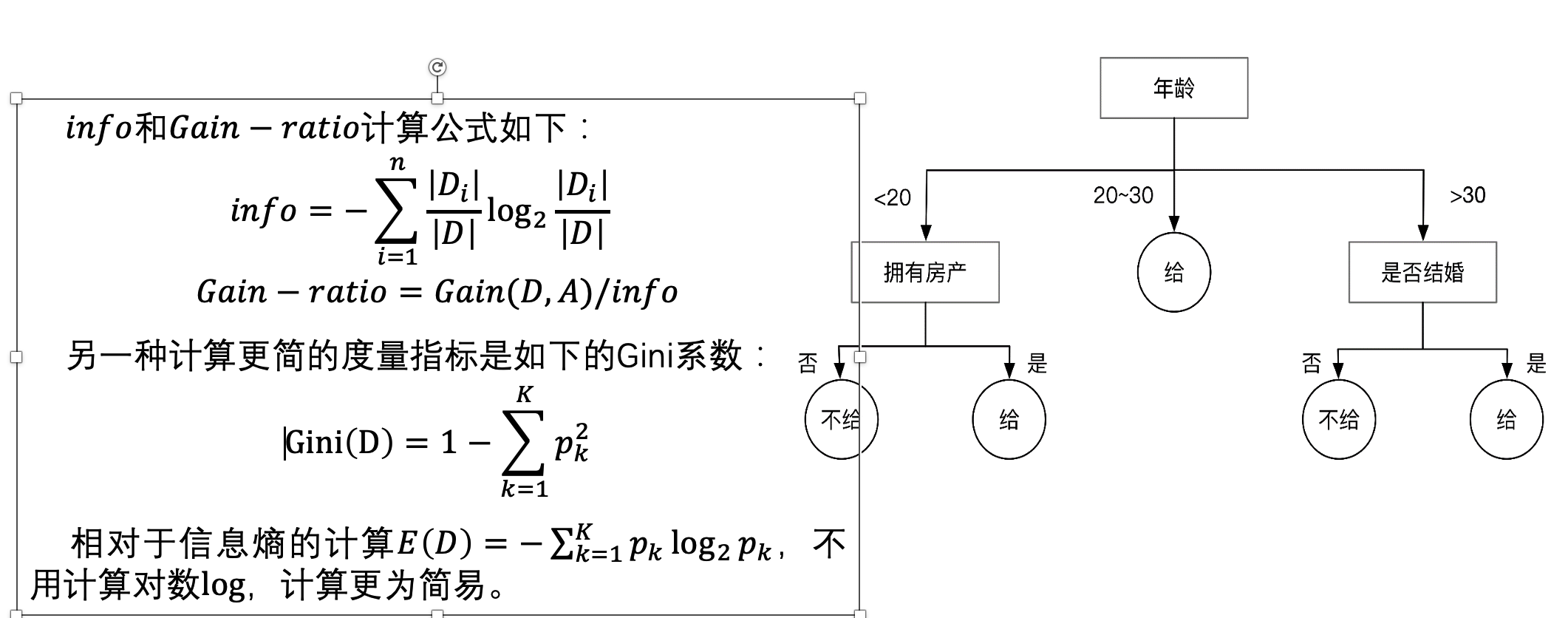
决策树是在干什么呢?选择最佳属性对样本进行划分,得到最大的“纯度”
同时注意决策树是有监督学习。
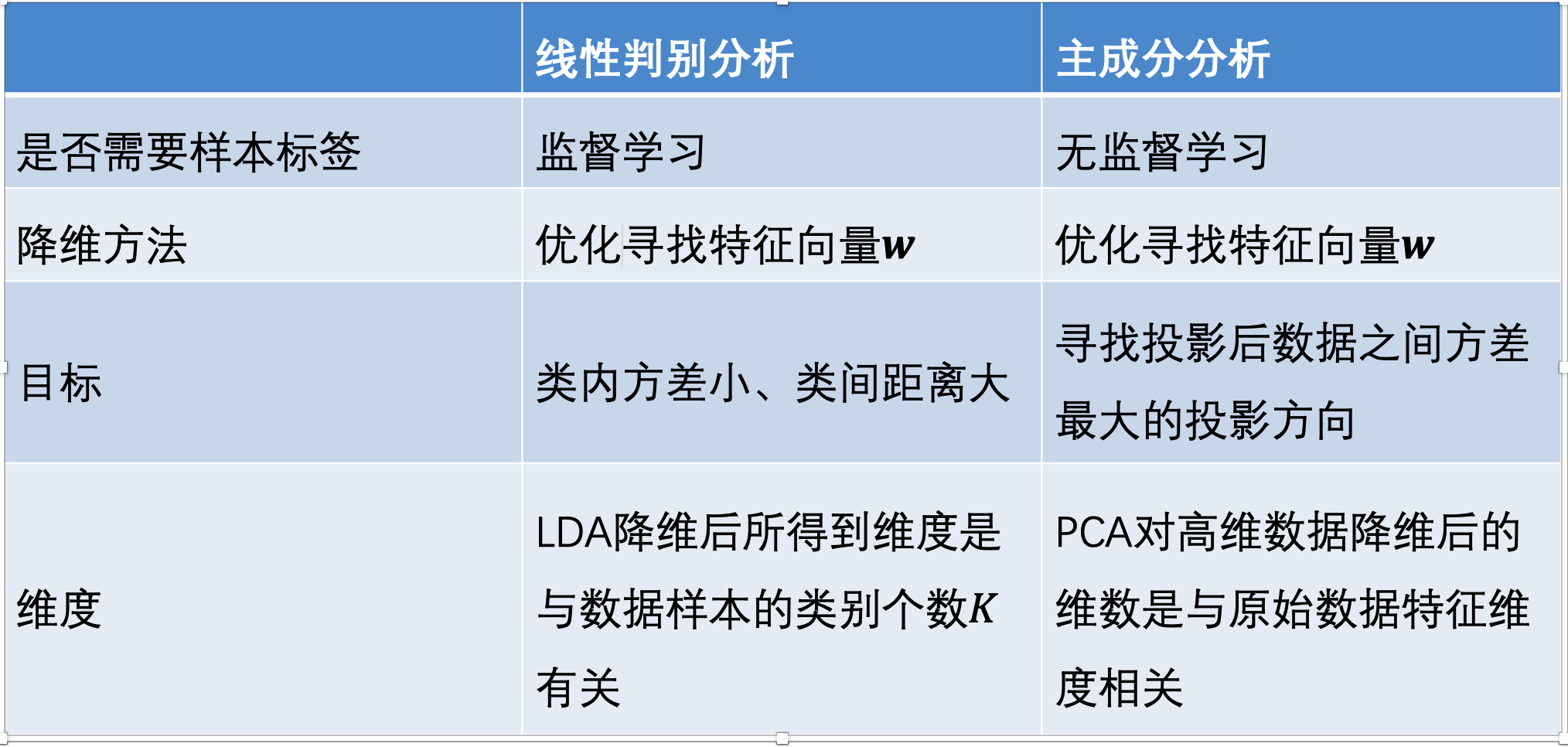
线性区别分析 (linear discriminant analysis, LDA)
线性判别分析的核心:类内方差小,类间间隔大。“君子和而不同,小人同而不和”,是一种降为方法
#请判断下面说法是否正确: 线性判别分析是在最大化类间方差和类内方差的比值(√)
#在一个监督学习任务中,每个数据样本有 4个属性和一个类别标签,每种属性分别有3、 2、2和2种可能的取值,类别标签有3种不同的取值。请问可能有多少种不同的样本?(注意,并不是在某个数据集中最多有多少种不同的样本,而是考虑所有可能的样本)()
乘起来就可以。72

记住就可以
重点:


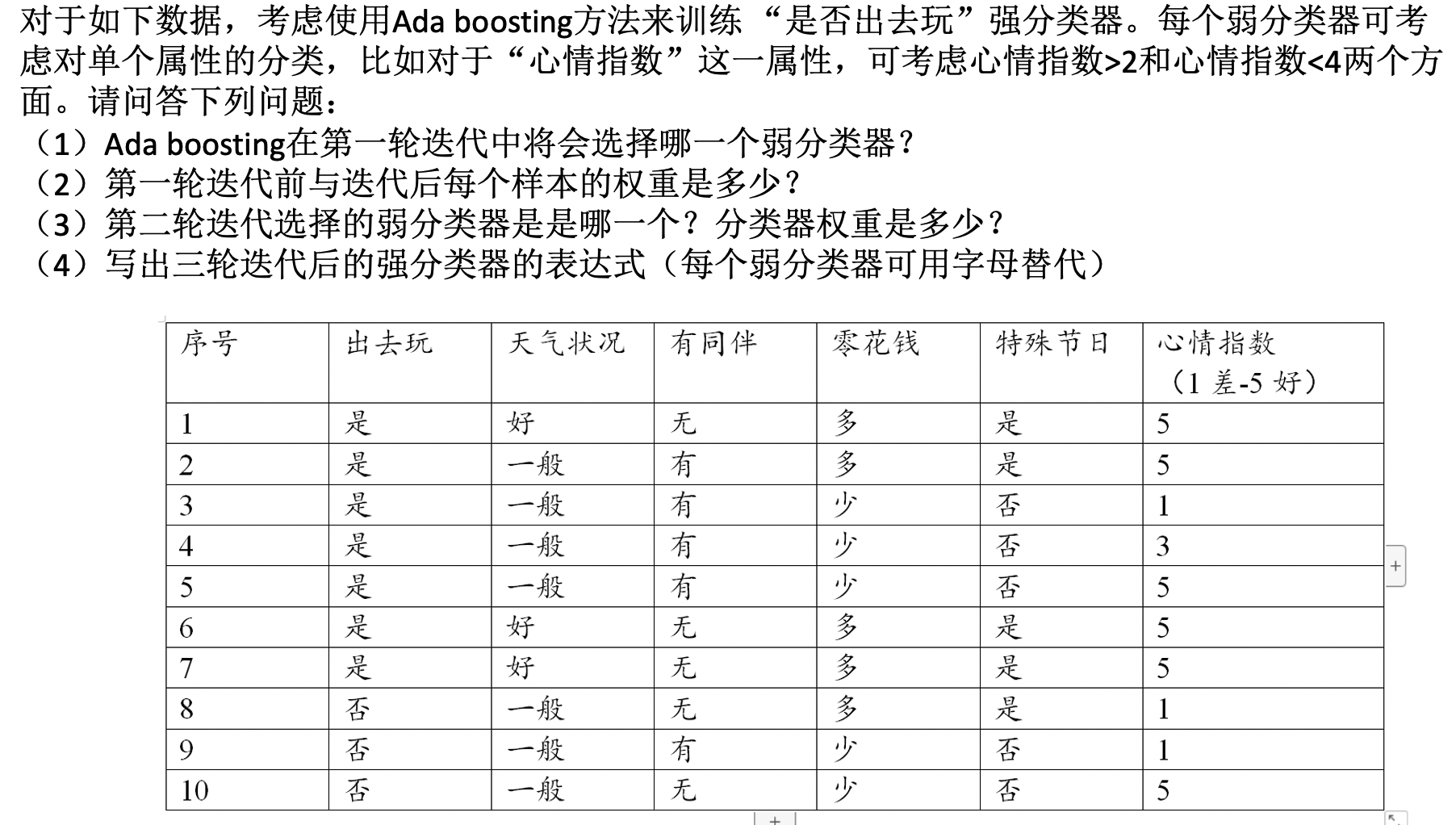
ada boosting
\(Z_m=\sum_{i=1}^N w_{m, i} \mathrm{e}^{-\alpha_m y G_i\left(x_i\right) \text { 。 }}\) 可以把对第 \(i\) 个训练样本更新后的分布权重写为如下分段函数形式: \[ w_{m+1, i}= \begin{cases}\frac{w_{m, i}}{Z_m} \mathrm{e}^{-\alpha_m}, & G_m\left(x_i\right)=y_i \\ \frac{w_{m, i}}{Z_m} \mathrm{e}^{\alpha_m}, & G_m\left(x_i\right) \neq y_i\end{cases} \] 可见, 如果第 \(i\) 个训练样本无法被第 \(m\) 个弱分类器 \(G_m(x)\) 分类成功, 则需要增大该样本权重, 否则减少该样本权重。这样, 被错误分类样本 会在训练第 \(m+1\) 个弱分类器 \(G_{m+1}(x)\) 时被 “重点关注”。
在第 \(m\) 次迭代中, Ada Boosting 总是趋向于将具有最小误差的学习模型(err最小的)选做本轮次生成的弱分类器 \(G_m\), 促使累积误差快速下降。
无监督学习
K-means往往找都是一个局部最优
聚类迭代满足如下任意一个条件,则聚类停止:
•已经达到了迭代次数上限
•前后两次迭代中,聚类质心基本保持不变


应当是尽量“不相关”
•主成分分析是将𝑛维特征数据映射到𝑙维空间(n≫l),去除原始数据之间的冗余性(通过去除相关性手段达到这一目的)。每一维的样本方差尽可能大
•特征人脸方法是一种应用主成份分析来实现人脸图像降维的方法,其本质是用一种称为“特征人脸(eigenface)”的特征向量(而不是像素)按照线性组合形式来表达每一张原始人脸图像,进而实现人脸识别。
每一个特征人脸的维数与原始人脸图像的维数一样大x 会变小
特征人脸之间的相关度要尽可能大√
为了使算法更高效采用了奇异值分解的方法

批量梯度下降算法是在整个训练集上计算损失误差C()。如果数据集较大,则会因内存容量不足而无法完成,同时这一方法收敛速度较慢。随机梯度下降算法是使用训练集中每个训练样本计算所得C()来分别更新参数。虽然,随机梯度下降收敛速度会快一些,但可能出现所优化目标函数震荡不稳定现象。

\[ f(x)=\frac{1}{1+\mathrm{e}^{-x}} \] 选取 sigmoid函数作为激活函数, 因为其具有如下优点: (1) 概率形式输出, sigmoid函数值域为 \((0,1)\), 因此使 sigmoid函数输出可视为概 率值; (2) 单调递增, sigmoid函数对输人 \(x\) 取值范围没有限制, 但当 \(x\) 大 于一定值后, 函数输出无限趋近于 1 , 而小于一定数值后, 函数输出无限趋近于 0 , 特别地, 当 \(x=0\) 时, 函数输出为 \(0.5\); (3) 非线性变化, \(x\) 取 值在 0 附近时, 函数输出值的变化幅度比较大 (函数值变化陡峭), 意味 着函数在 0 附近容易被激活且是非线性变化, 当 \(x\) 取值很大或很小时, 函数输出值几乎不变, 这是基于概率的一种认识与需要。






强化学习的特征


一个随机过程实际上是一列随时间变化的随机变量。当时间是离散 量时, 一个随机过程可以表示为 \(\left\{X_t\right\}_{t=0,1,2, \cdots}\), 这里每个 \(X_t\) 都是一个随机变量, 这被称为离散随机过程。为了方便分析和求解, 通常要求通过合理的问题定义使得一个随机过程满足马尔可夫性 (Markov property), 即满足如下性质: \[ P\left(X_{t+1}=x_{t+1} \mid X_0=x_0, X_1=x_1, \cdots, X_t=x_t\right)=P\left(X_{t+1}=x_{t+1} \mid X_t=x_t\right) \text { (式7.1) } \] 这个公式的直观解释为: 下一刻的状态 \(X_{t+1}\) 只由当前状态 \(X_t\) 决定 (而与更早的所有状态均无关)。满足马尔可夫性的离散随机过程被称为 马尔可夫链 (Markov chain)。
- 动作 \(-\) 价值函数 (action-value function): \(q: S \times A \mapsto \mathbb{R}\), 其中 \(q_\pi(s, a)=\mathbb{E}_\pi\left[G_t \mid S_t=s, A_t=a\right]\), 表示智能体在时刻 \(t\) 处于状态 \(s\) 时, 选择 了动作 \(a\) 后,在 \(t\) 时刻后根据策略 \(\pi\) 采取行动所获得回报的期望。 价值函数和动作 \(-\) 价值函数反映了智能体在某一策略下所对应状态 序列获得回报的期望, 它比回报本身更加准确地刻画了智能体的目标。 注意, 价值函数和动作 \(-\) 价值函数的定义之所以能够成立, 离不开决策 过程所具有的马尔可夫性, 即当位于当前状态 \(s\) 时, 无论当前时刻 \(t\) 的取值是多少, 一个策略回报值的期望是一定的 (当前状态只与前一状态有 关,与时间无关)。(所以不是\(q_\pi(s, a,t)\)) 至此, 强化学习可以转化为一个策略学习问题, 其定义为: 给定一 个马尔可夫决策过程 \(M D P=(S, A, P, R, \gamma)\), 学习一个最优策略 \(\pi^*\), 对任 意 \(s \in S\) 使得 \(V_{\pi^*}(s)\) 值最大。