机器学习-模型评估与选择
模型评估与选择
模型评估方法
书后习题

经验误差和泛化误差
定义

解决过拟合现象:正则化

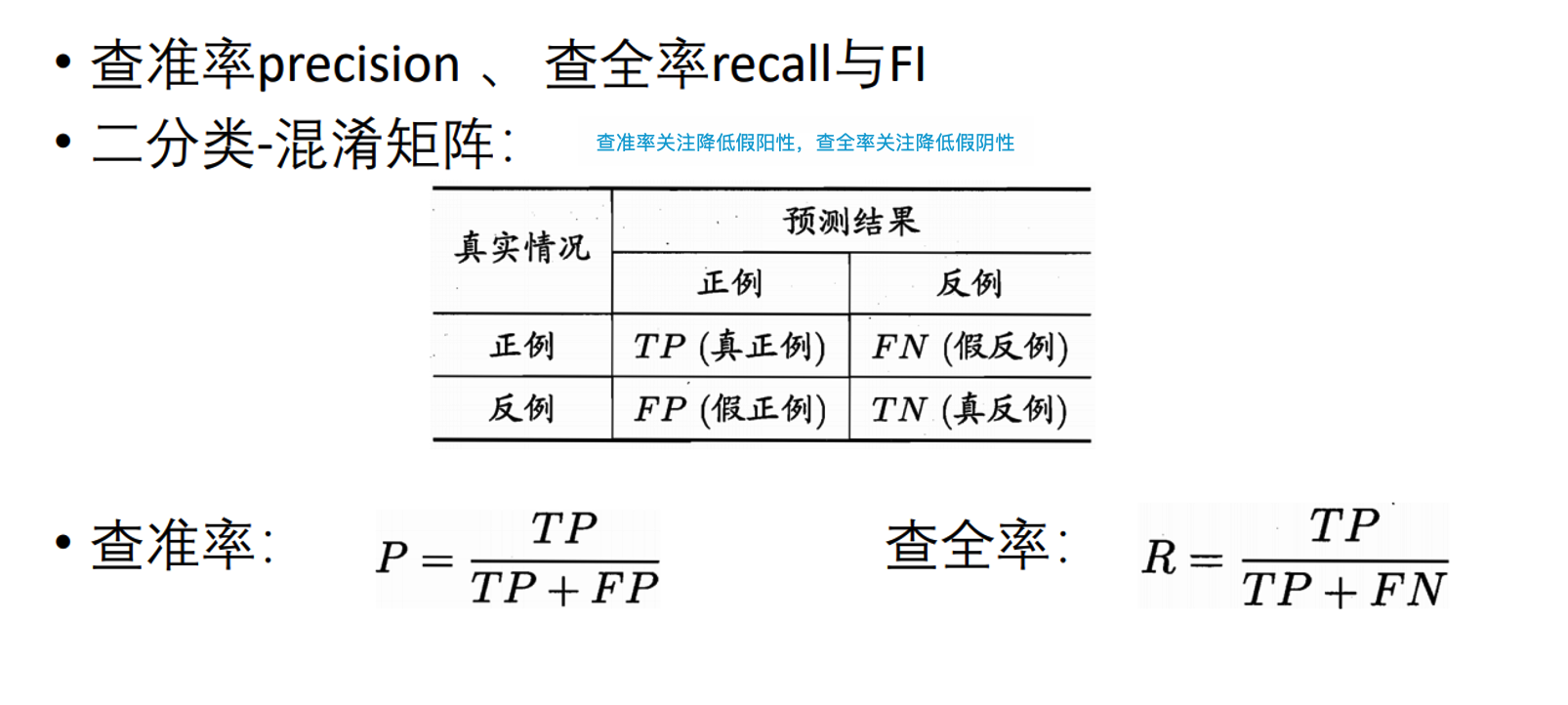
性能度量
基本概念
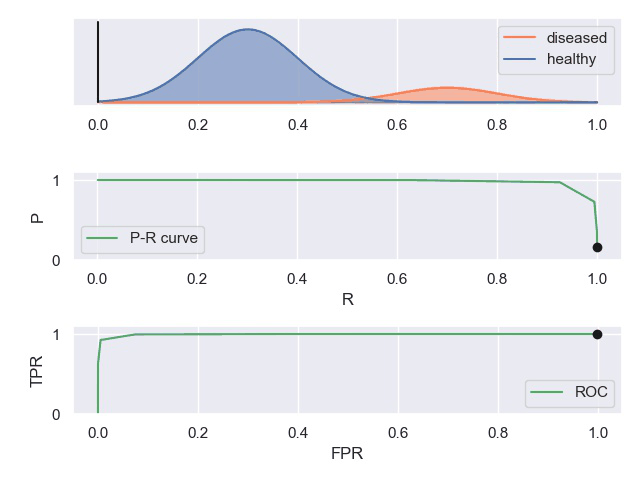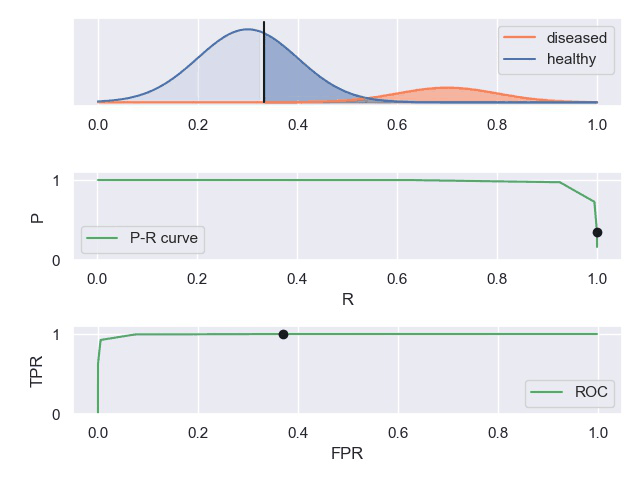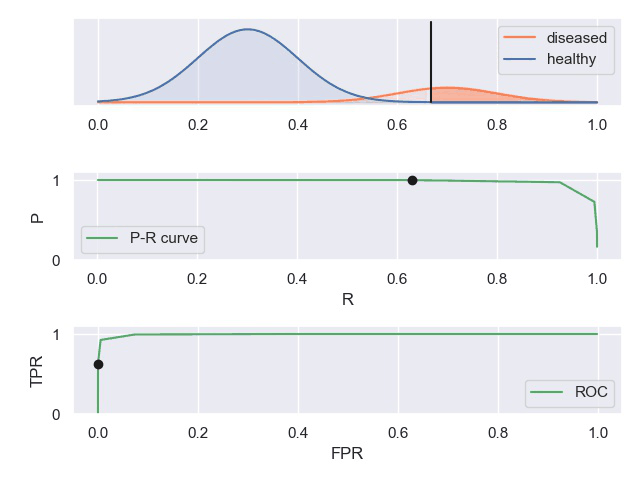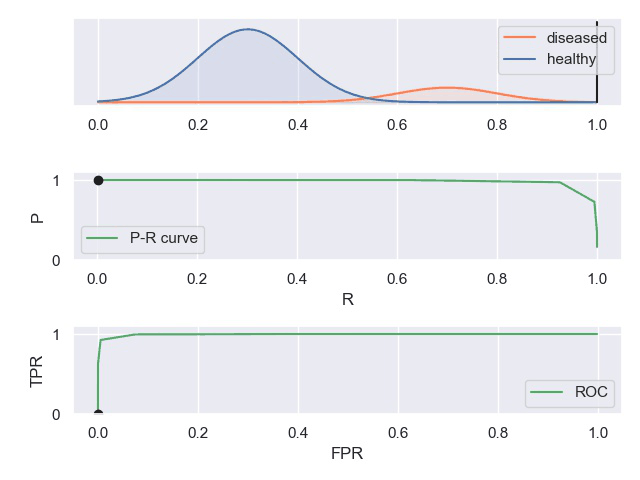
P-R曲线和ROC曲线
实例
知乎上有一个案例对这些曲线描述的比较形象。
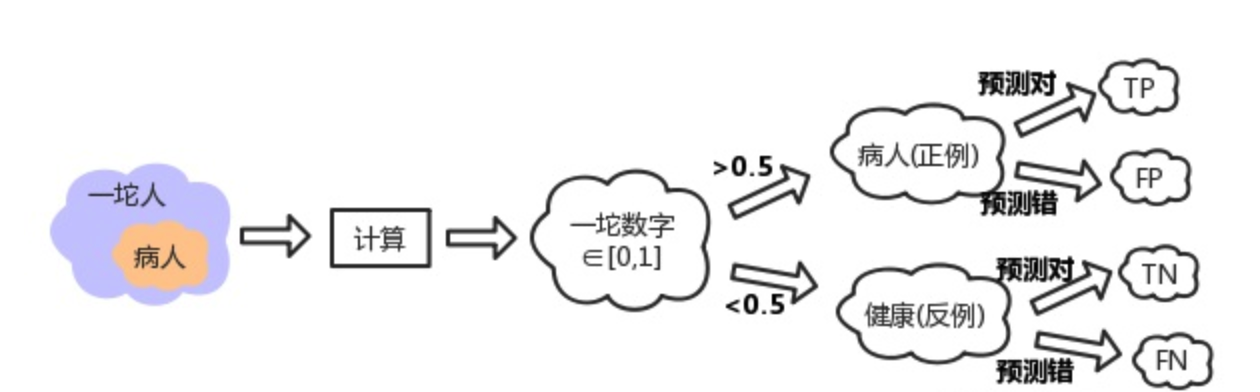

TPR真阳性,FPR假阳性
一个表现平平的分类器(表现是指分类标准能否将两种样本有效的分开,而threshold是指划分标准更倾向于查全率或准确率)
F1计算
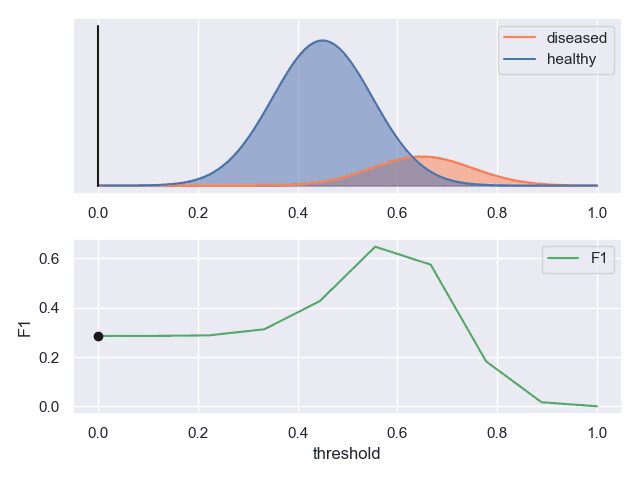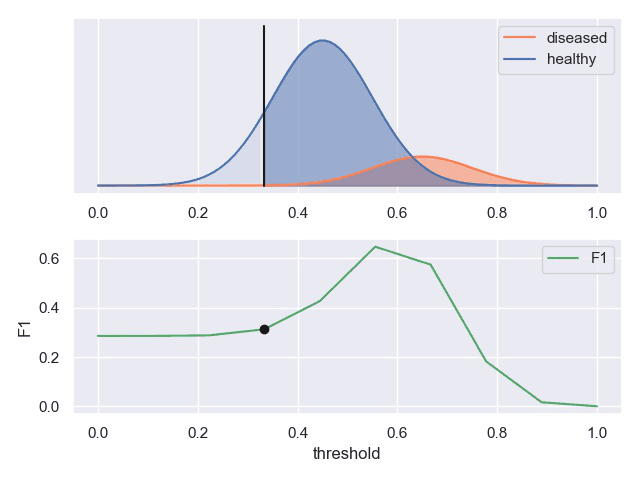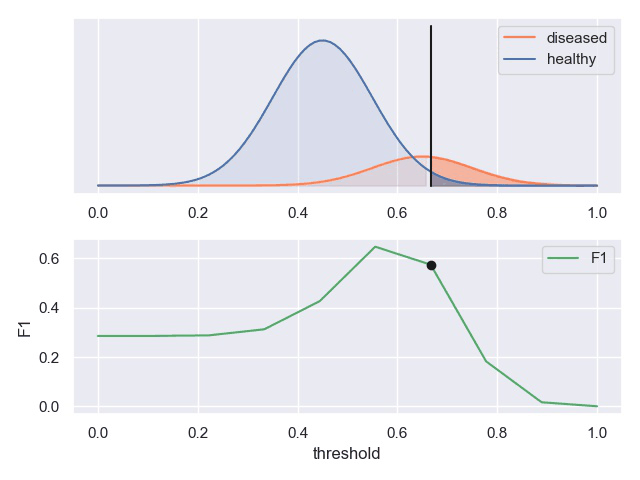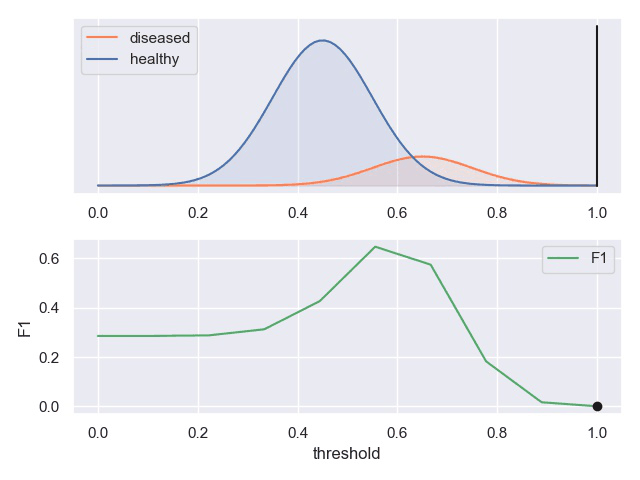
用途
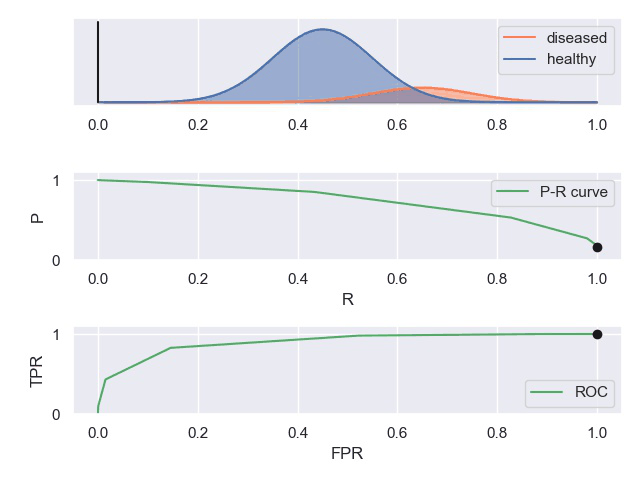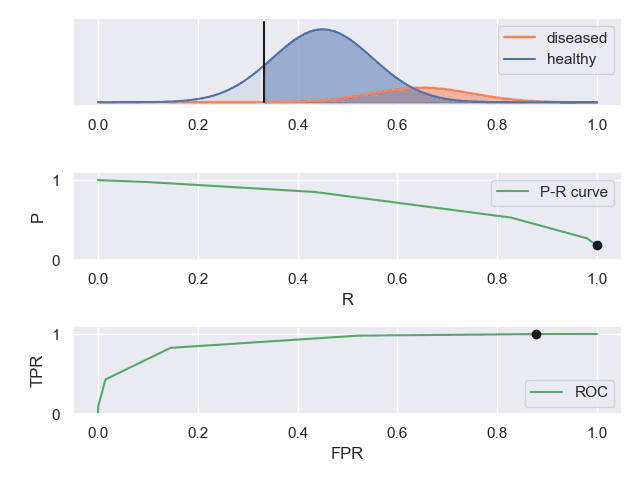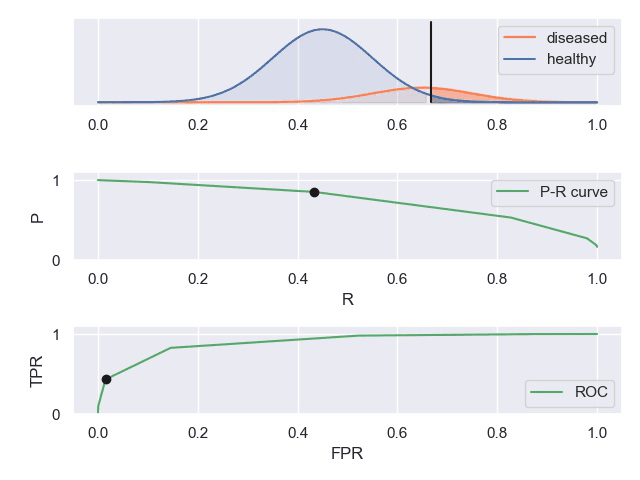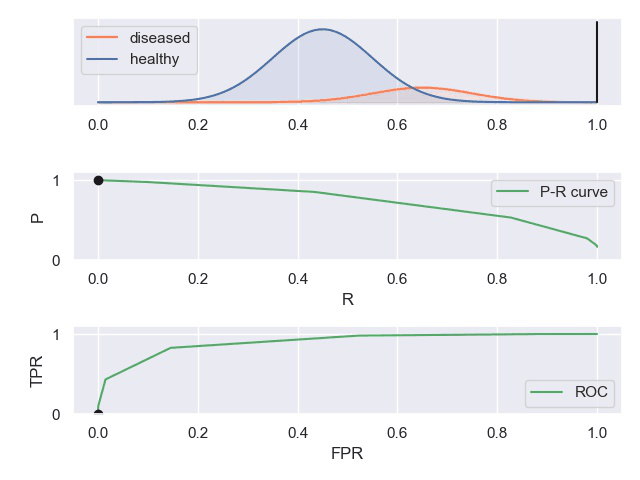
基于P-R曲线可以大致评判机器学习模型的好坏
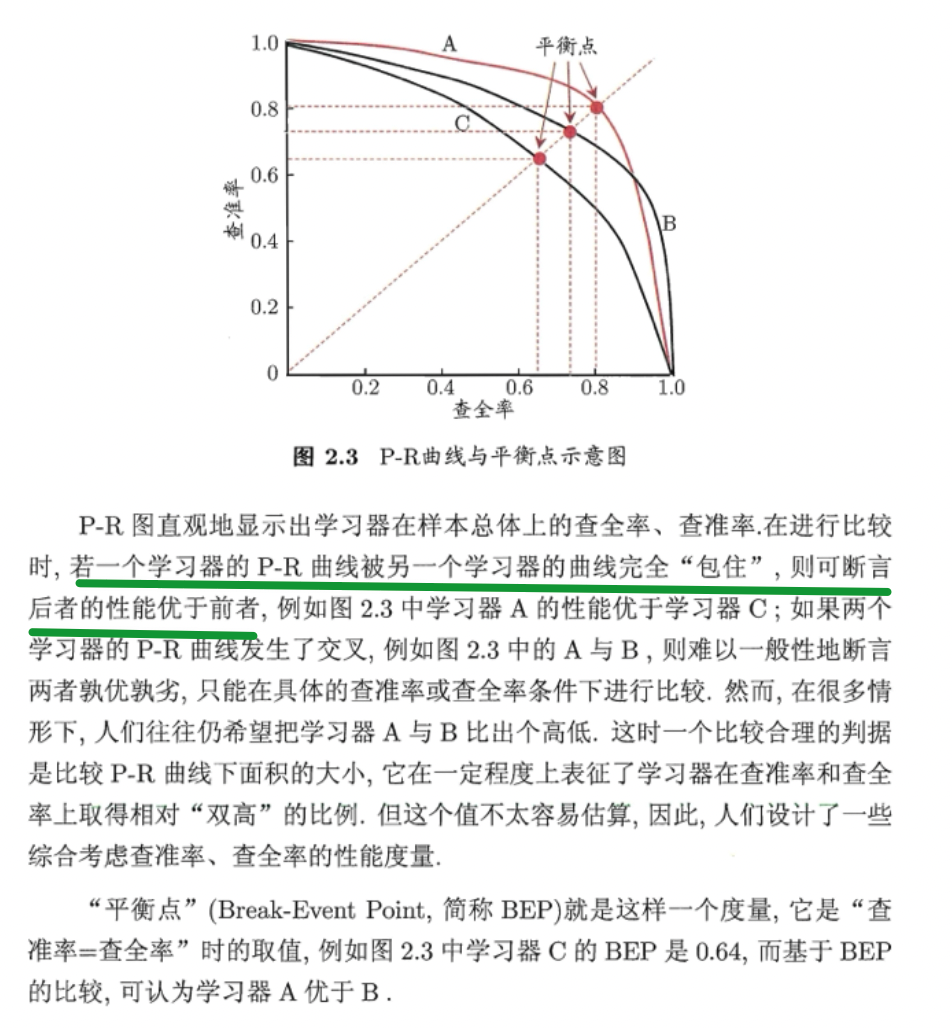
ROC也是如此。
从定义可知, AUC 可 通过对 ROC 曲 线下各部分的面积 求和而得.
形式化地看, AUC 考虑的是样本预测的排序质量。
习题:若学习器A的F1值比学习器B高,试析A的BEP值是否也比B高
二者是不同维度的指标。当然在达到BEP的条件时(P=R),F1的值和BEP相等。
ROC代价曲线
参考知乎答案
首先, 横坐标是 \(\mathrm{P}(+)\), 由公式3可以知道, 当 \(\mathrm{P}(+)=0\) 时, \({c o s t}_{n o r m}=\mathrm{FPR}\); 当 \(\mathrm{P}(+)=1\) 时, \(\operatorname{cost}_{n o r m}=\mathrm{FNR}_{\circ}\) 直白含义: 当我用来检测模型好坏的样本全是负例(即 $(+)=0 $) ,那我模型产生的错误就只有负例被错误的预测 为正例这一种情况, 就是 \((0, F P R)\) 。 同样, 当我用来检测模型好坏的样本全都是正例(即 $(+)=1 $ ),那我模型产生的错误就只有正例被错 误的预测为负例的情况这一种情况,就是 \((1, \mathrm{FNR})\) 两个连线中间的情况, 用来检测模型的样本有正例也有负例的时候, 也就是 \(P(+)=0 . x\), 这时候 \(\operatorname{cost}_{n o r m}\) 的取值就会同时受到FPR和FNR的影响。
很像高中化学读图题的定性分析:
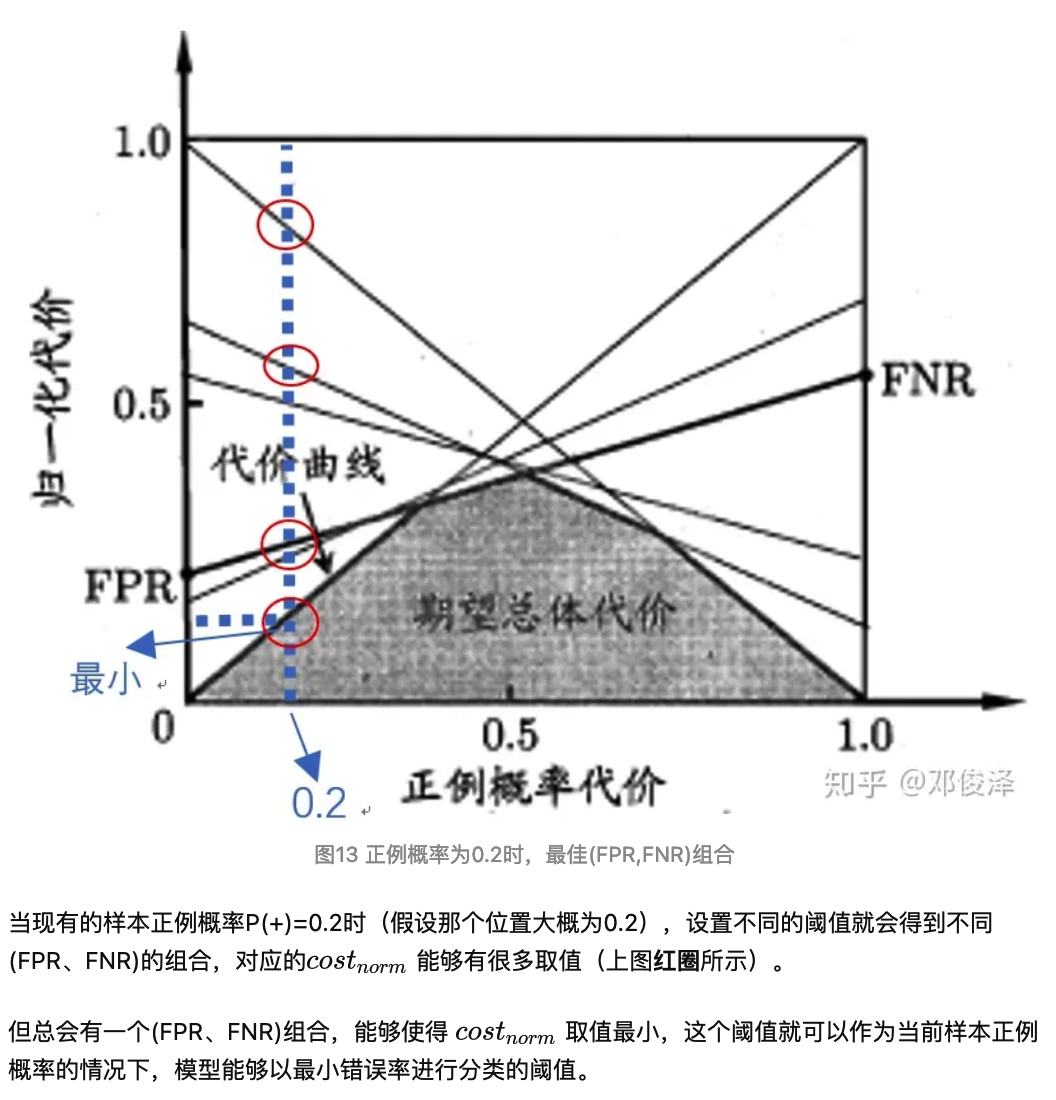

就像做核酸”粉饰太平“一样( \[ P(+)=\frac{p \cdot \cos _{0 \mid 1}}{p \cdot \operatorname{cost}_{0 \mid 1}+(1-p) \cdot \operatorname{cost}_{1 \mid 0}} \] \(\operatorname{cost}_{0 \mid 1}\) 表示: 实际为正类, 而错判成负类的代价, \(\operatorname{cost}_{1 \mid 0}\) 表示: 实际为负类, 而错判成正类类Q 的代价。 举例说明, 当我们认为, 正例错判为负例的代价与负例错判为正例的代价相同时, \(P^1(+)=p\) 当我们认为把正类判定为负类会造成更大的损失时(比如假设核酸检测瞒报比误报代价更大), 此时 \(\operatorname{cost}_{1 \mid 0}>;\cos t_{0 \mid 1}\), 带入正例代价公式 得 \(P^2(+)\), 这时候就有 \(P^2(+)>;P^1(+)\) 。 对应到ROC代价图, 正例概率 \(P(+)\) 就会往左移动, 对应的阈值就会减小, 模型对负类的判断就会更谨慎(比如下调CT值)。

\(\beta\)>1时查全率有更大影响;\(\beta\)<1时查准率有更大影响。
(核酸检测评价假设偏向减少瞒报,则\(\beta>1\))
比较检验
单边t检验和成对t检验可以分别用于评价单个学习器的错误率和比较两个学习器的性能。
对二分类问题,使用留出法不仅可估计出学习器 A 和 B 的测试错误率,还可获得两学习器分类结果的差别,使用McNemar 检验可以做到。

$Min-max $规范化优点:1、计算相对简单一点。2、当新样本进来时,只有在新样本大于原最大值或者小于原最小值时,才需要重新计算规范化之后的值。缺点在于:1、容易受高杠杆点和离群点影响。
\(z-score\) 规范化优点:1、对异常值敏感低。缺点在于:1、计算更负责。2、每次新样本进来都需要重新计算规范化。
偏差方差分解
用途:解释算法泛化性能来源的手段 \[ E(f ; D)=\operatorname{bias}^2(\boldsymbol{x})+\operatorname{var}(\boldsymbol{x})+\varepsilon^2, \] 也就是说, 泛化误差可分解为偏差、方差与噪声之和。
注意这个式子的推导,详见南瓜书。
- 「偏差」度量了学习算法的期望预测与真实结果的偏离程度,即「刻画了学习算法本身的拟合能力」;
- 「方差」度量了同样大小的训练集的变动所导致的学习性能的变化,即「刻画了数据扰动所造成的影响」;
- 「噪声」则表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界,即「刻画了学习问题本身的难度」.
偏差一方差分解说明,泛化性能是由「学习算法的能力」、「数据的充分性」以及「学习任务本身的难度所共同决定」的。
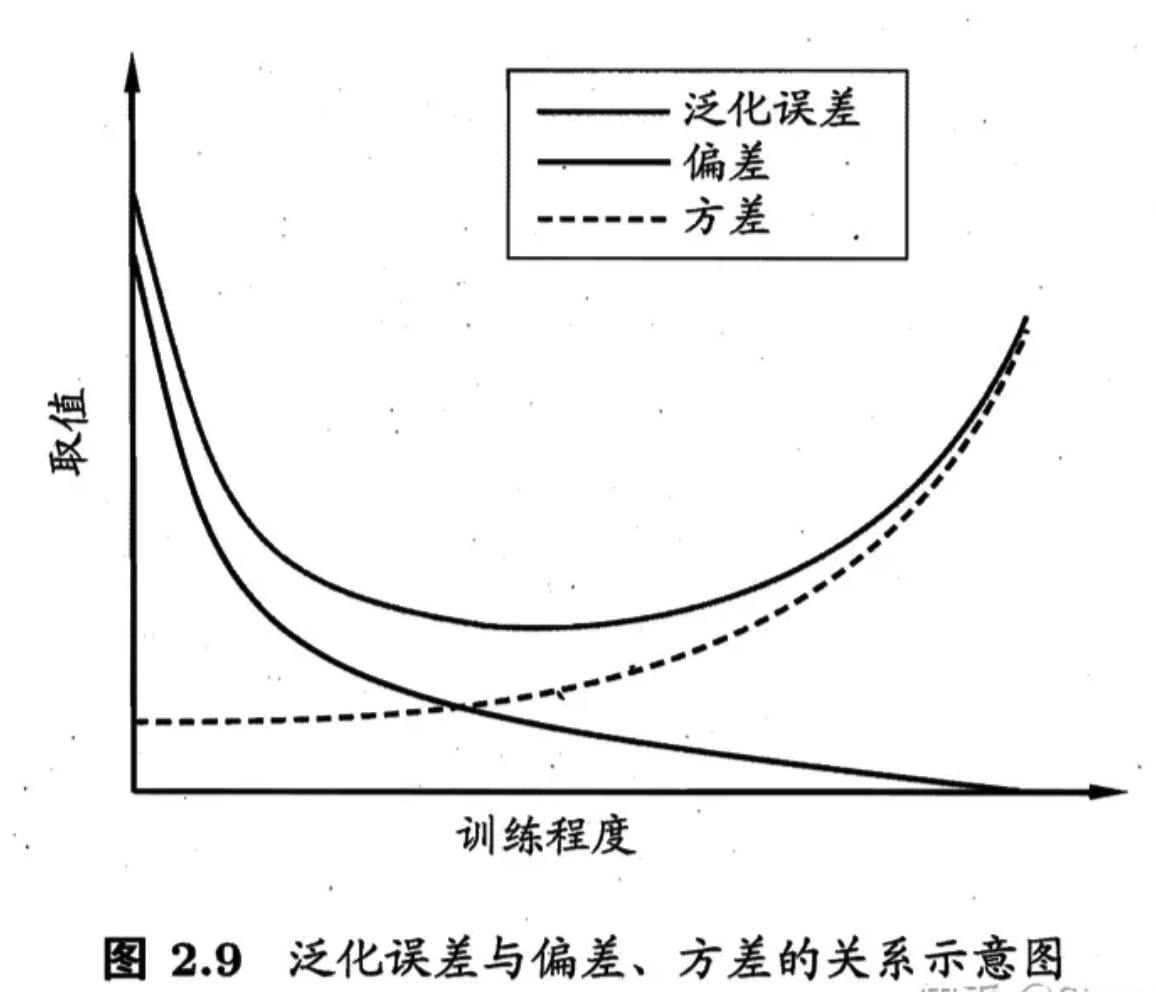
随训练强度,偏差减小,方差增大,即学习的越充分,但受数据影响越大,可能出现过拟合现象。