编译原理-词法分析
编译原理-词法分析
正则表达式
注意课上没提到的正则写法,仅作为了解
\w 用于查找字母、数字和下划线
\W 匹配除字母、数字和下划线之外的字符
\d 仅用来匹配数字
\D用来匹配数字之外的所有字符
\s 仅匹配空白字符

首尾符号不同的a、b串
(a(a*b)+) | (b(b*a)+)
或(a(a|b)*b) | (b(a|b)*a)首尾符号相同的a、b串 包括只有a或b的情况
(a(b*a)*)|(b(a*b)*)NFA设计
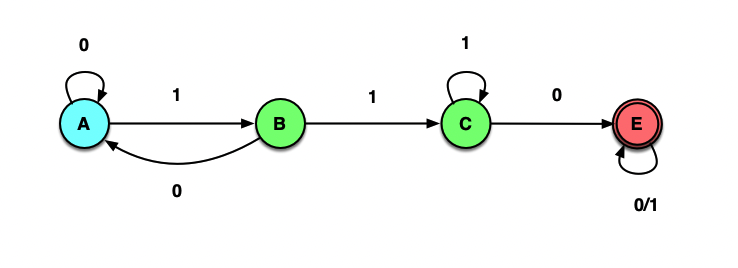
不包含字串011的01串
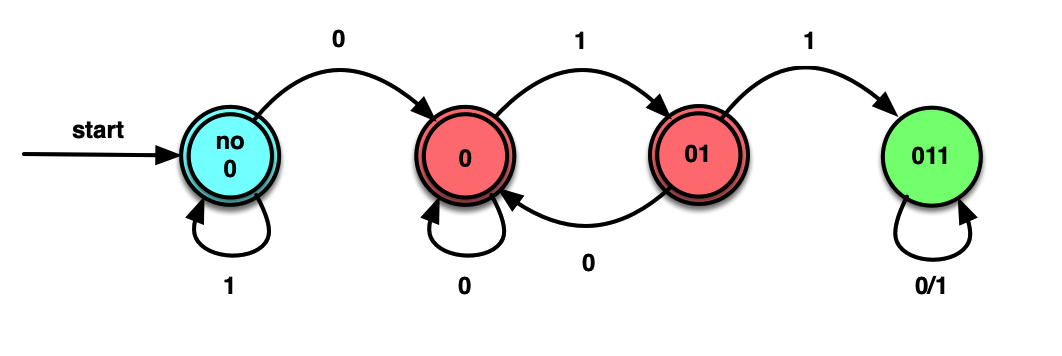
偶数个0,偶数个1的0/1串
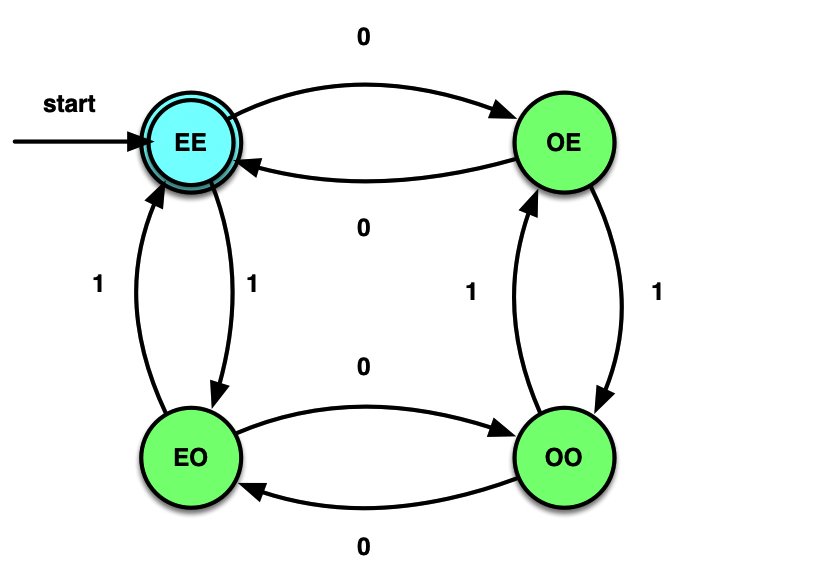
能被3整除的二进制串
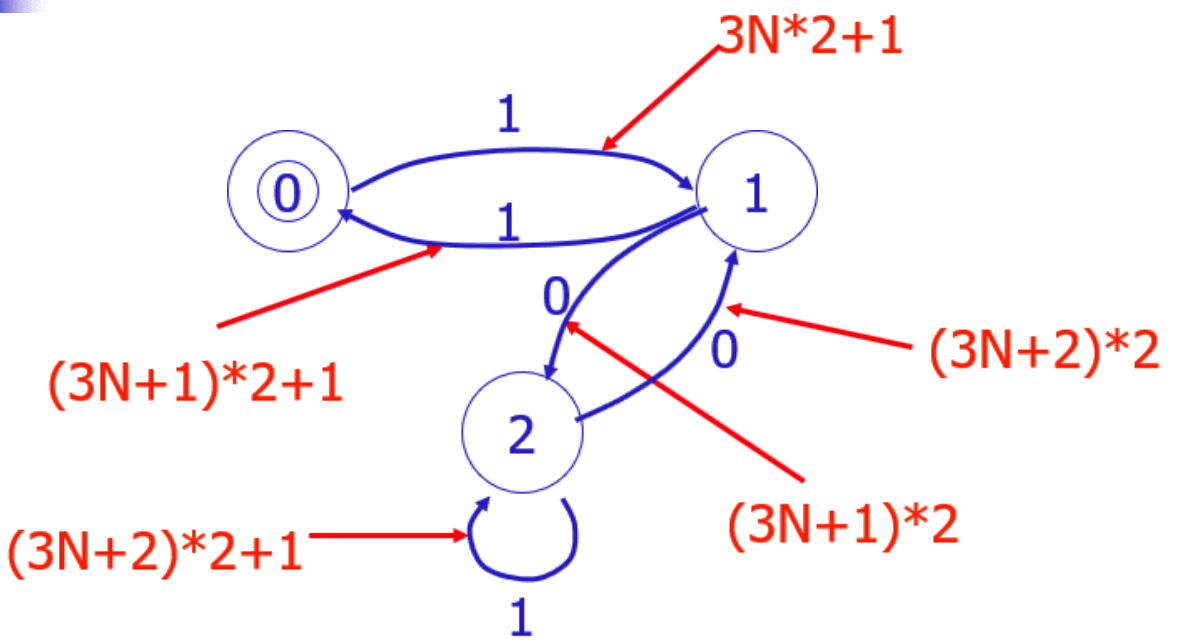
正则-NFA
Thomson 构造法。基本思想是递归:
对于基本的 re,直接构造
对于复合的 re,递归构造
具体构造方式比较简单,在此略去
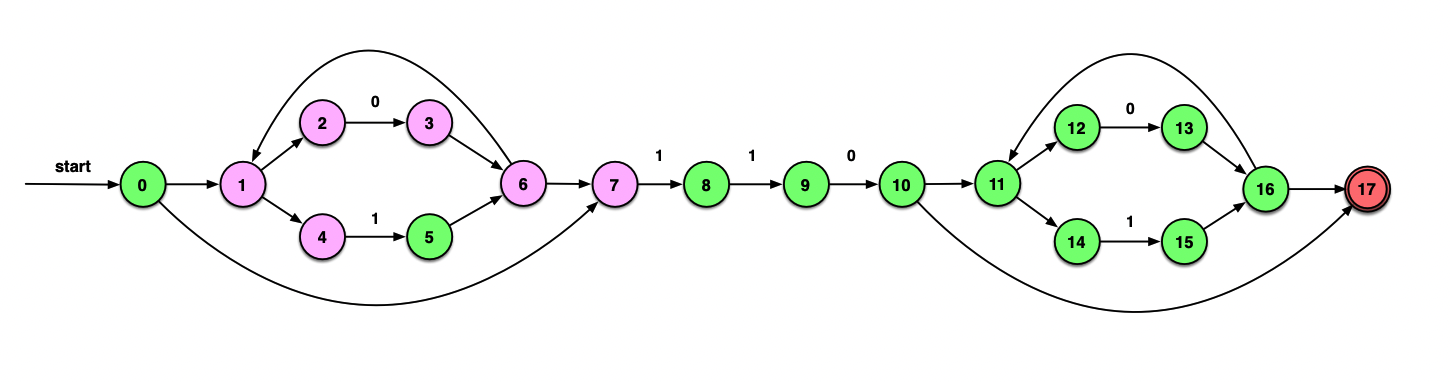
以(0 | 1)*110(0 | 1)*为例:
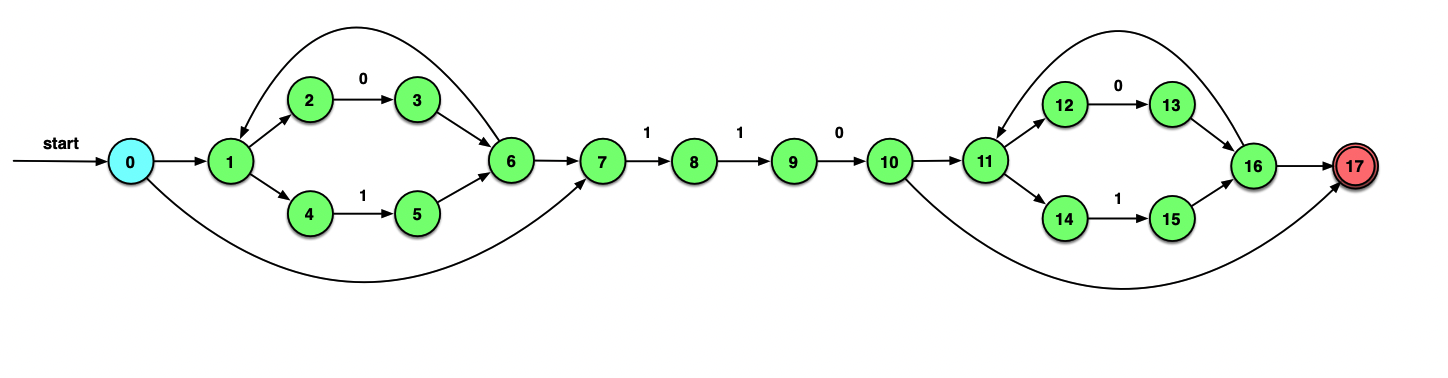
NFA-DFA
子集构造法
算法理解:
递推的思想
最简单的符号串ε:NFA状态集合←→DFA 状态
长度为1的串a=εa,在自动机中可达的状态为:从c对应的状态经过标记为a的边可达的状态
长度为2的串...
算法需要注意的地方:
DFA新的状态对应NFA状态集消耗一个字符,能够走到的状态集。所以很明显,这里要消耗,所以不能是 ε,并且只能消耗一个。
得到步骤 1 中的状态集之后,还需要考虑,这里面的所有节点,通过 ε 能走到的所有状态。注意,这里的每个状态,只要可以通过 ε 走,就必须一直走下去,也就是所谓的
ε-闭包。这一步得到状态集的就是最后的结果。第二步需要格外注意的是别忘了检查克林顿闭包中往回返的边。
只要包含了NFA中的终态,在DFA中就作为终态出现。
直到检查某一个状态的ε-闭包不再产生新状态的时候,算法停止。
实例
上面的图进行一遍子集构造的过程(往年的期末考题,推导过程要比课上讲的例子长一些,小心出错)

先考虑空串:
ε_closure({0})={0, 1, 2, 4, 7}=A
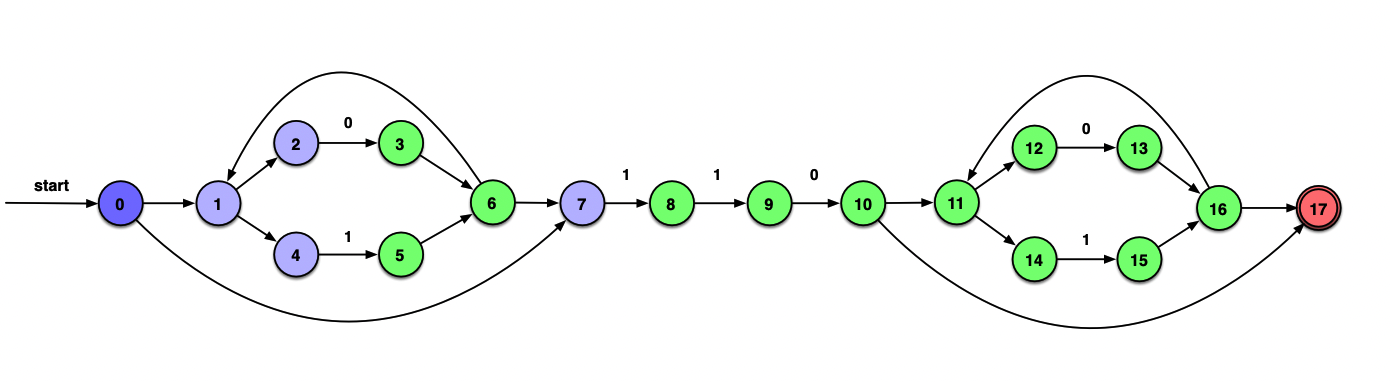
在DFA里加入开始状态A。
由于只有2有能够消耗0的边,因此下一步从这个状态指向的3开始考虑:
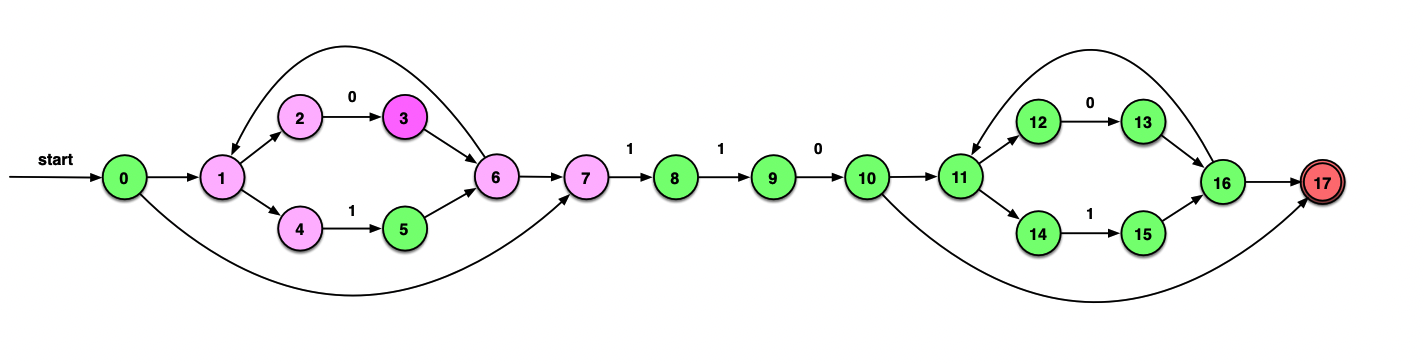
ε_closure(δ(A, 0))=ε_closure({3})={3, 6, 7, 1, 2, 4}={1, 2, 3, 4, 6, 7}=B
同理。不过这一次在A中4和7都能提供消耗1的边,因此要从5和8开始拓展两次ε_closure:
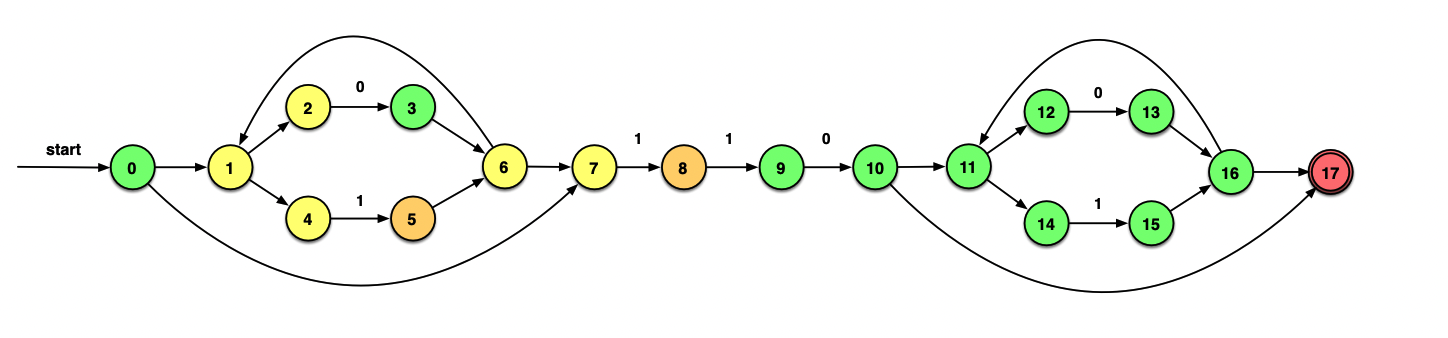
ε_closure(δ(A, 1))=ε_closure({5,8})={5, 6, 7, 1, 2, 4, 8}={1, 2, 4, 5, 6, 7, 8}=C
考虑了所有消耗一个字符的情况后,我们的DFA应当是这个样子:
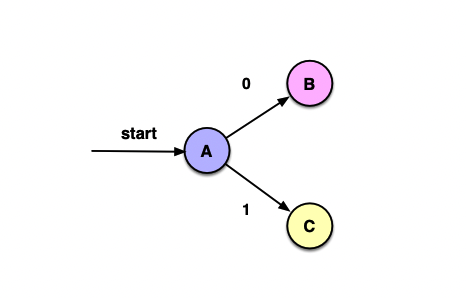
B状态消耗0的状态是{3}。而{3}的ε闭包我们已经求过,它就是B:
ε_closure(δ(B, 0))=ε_closure({3})=B
同样的,B消耗1后为{5,8},它的ε闭包我们也是知道的,是C。
ε_closure(δ(B, 1))=ε_closure({5,8})=C
那么有:
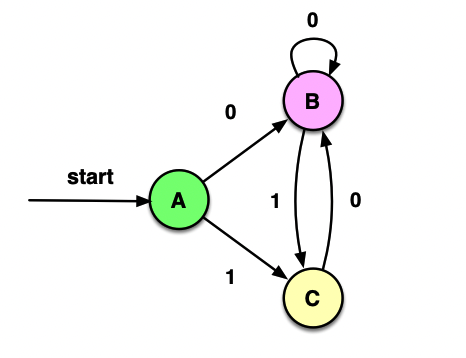
再来考察C:
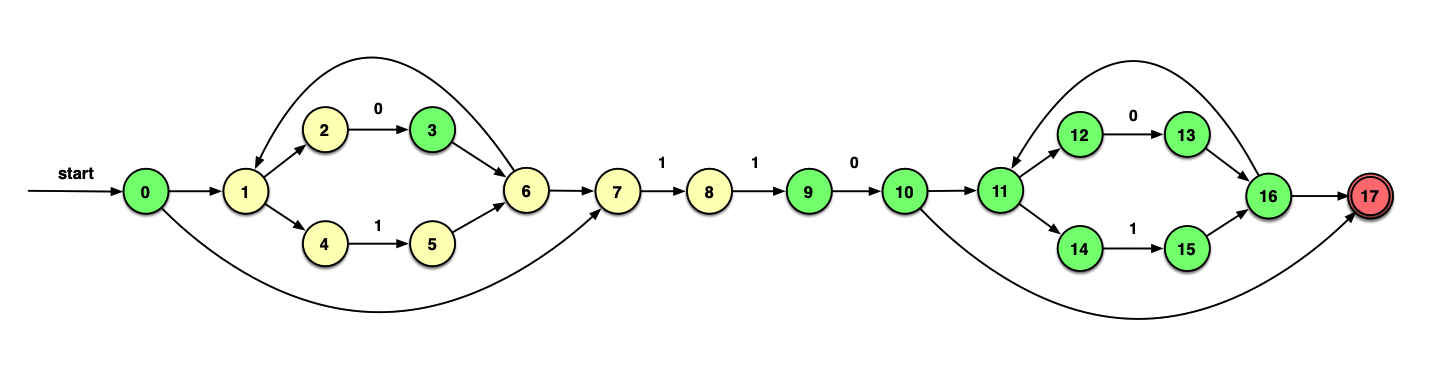
ε_closure(δ(C, 0))=ε_closure({3})=B
ε_closure(δ(C, 1))=ε_closure({5,8,9})={5, 6, 7, 1, 2, 4, 8, 9}={1, 2, 4, 5, 6, 7, 8, 9}=D
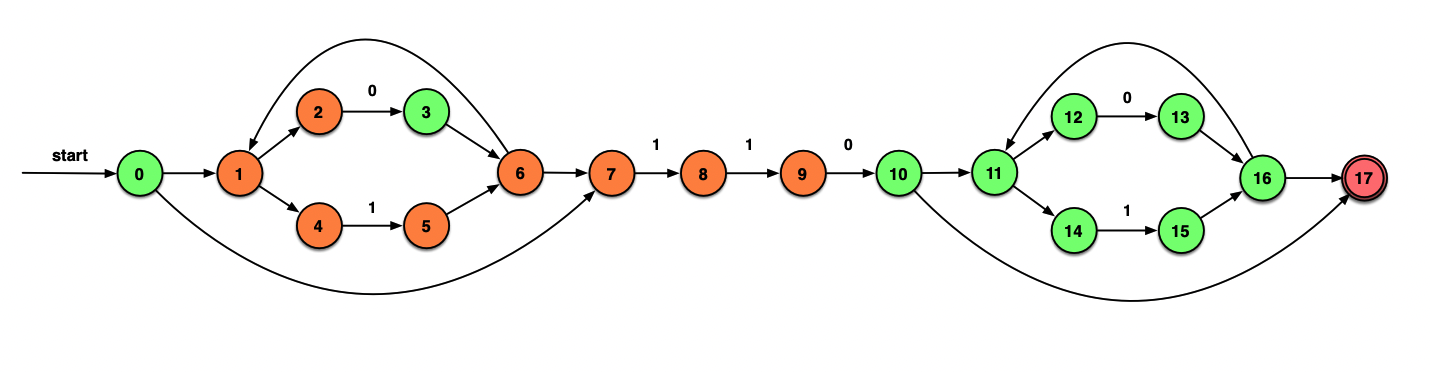
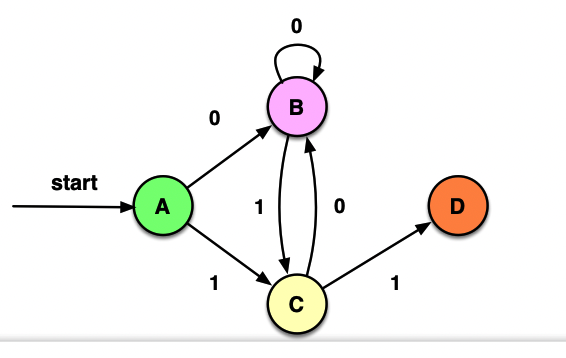
考察新状态D:
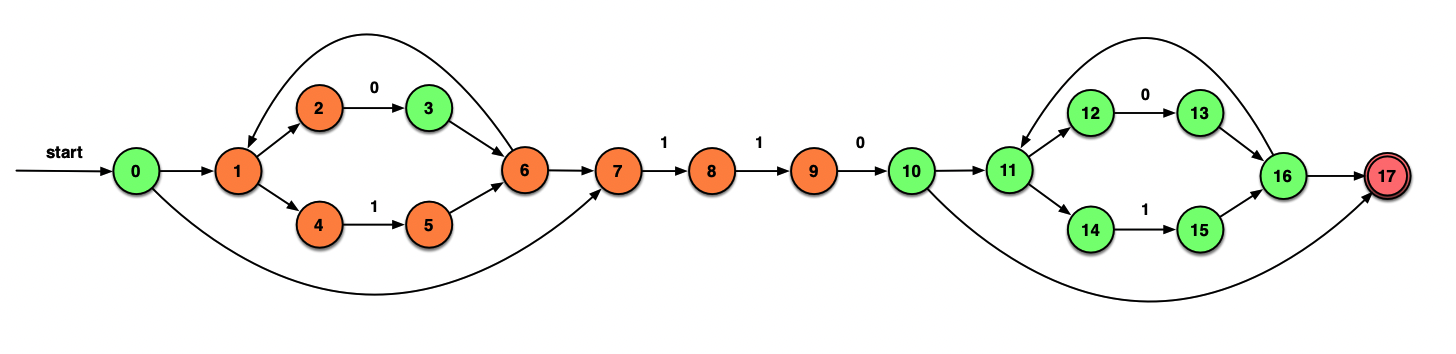
ε_closure(δ(D, 0))=ε_closure({3,10})={3, 6, 7, 1, 2, 4, 10, 11, 12, 14, 17}={1, 2, 3, 4, 6, 7, 10, 11, 12, 14, 17}=E
这一次覆盖的状态包含了终态17.因此在DFG中E就要加一个圈,表示终态。
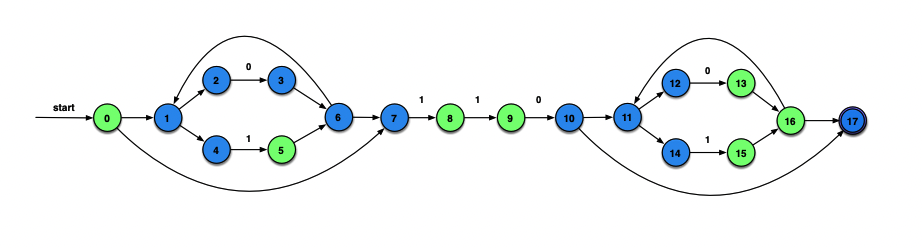
ε_closure(δ(D, 1))=ε_closure({4,7,8})=D
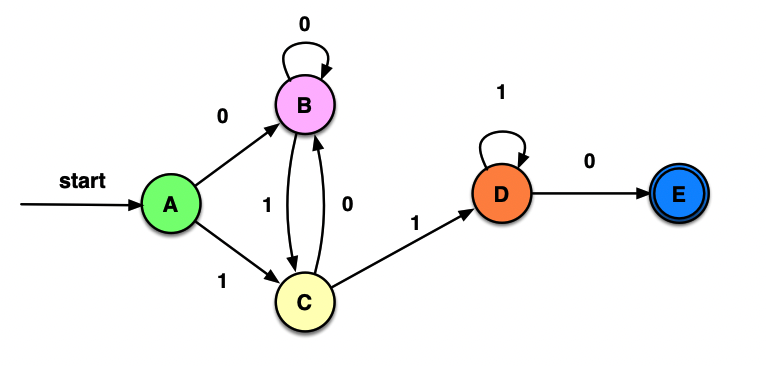

ε_closure(δ(E, 0))=ε_closure({3,13})={1, 2, 3, 4, 6, 7, 11, 12, 13, 14, 16, 17}=F
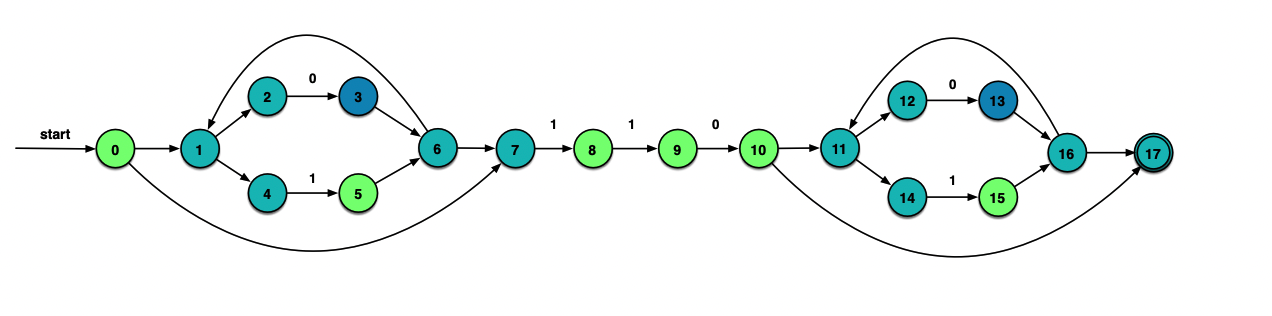
ε_closure(δ(E, 1))=ε_closure({5,8,15})={ 1, 2, 4, 5, 6, 7, 8, 11, 12, 14, 15, 16, 17}=G
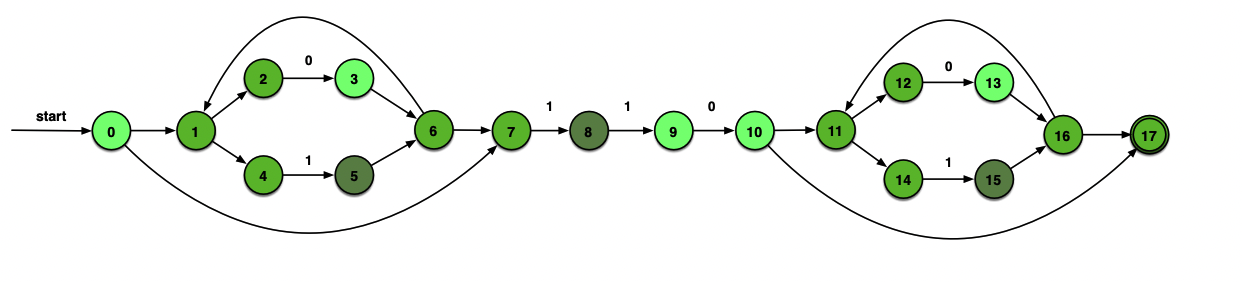

ε_closure(δ(F, 0))=ε_closure({3,13})=F
ε_closure(δ(F, 1))=ε_closure({5,8,15})=G

ε_closure(δ(G, 0))=ε_closure({3,13})=F
ε_closure(δ(G, 1))= ε_closure({5,8,9,15})={ 1, 2, 4, 5, 6, 7, 8, 9, 11, 12, 14, 15, 16, 17}=H
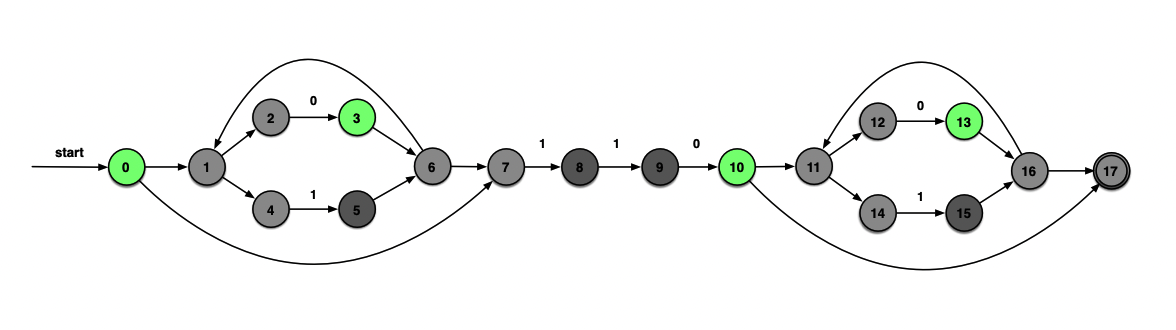
ε_closure(δ(H, 0))=ε_closure({3,10,13})={1, 2, 3, 4, 6, 7, 10, 11, 12, 13, 14, 16, 17}=I
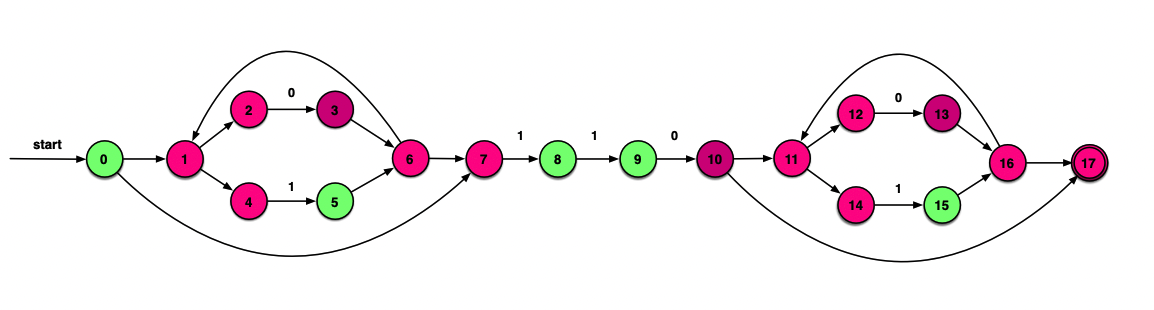
ε_closure(δ(H, 1))=H
ε_closure(δ(I, 0))=F
ε_closure(δ(I, 1))=G
发现I不再产生新的状态了,长舒一口气,终于可以结束了。
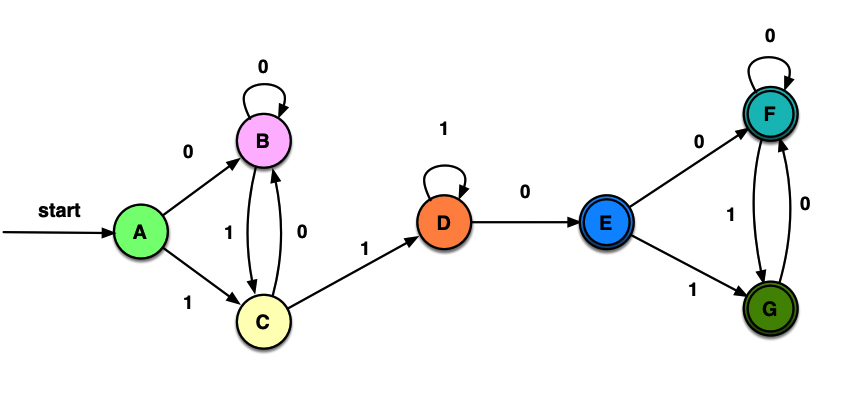
最终的DFA如下所示:
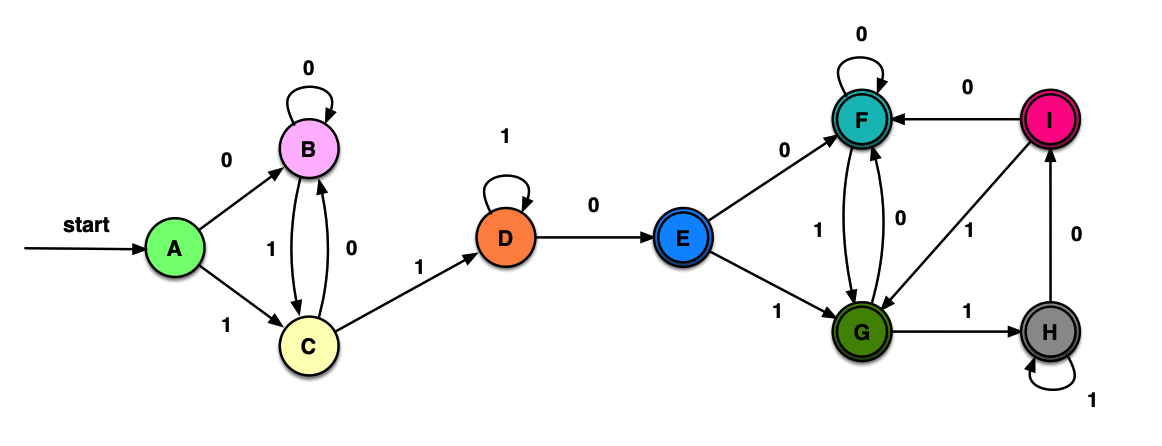
做题技巧:做到后面可以连同记下求过的ε_closure。A⊆B则ε_closure(A)⊆ε_closure(B)
识别0111010过程:A →B →C →D →D →E →G →F
DFA优化
优化思想
具有非ε的输出边的状态显然是NFA中的重要状态
δ(s,a)不空,当且仅当s是重要状态→ 决定了ε_closure(δ(T,a))的计算→子集构造法的核心
两个子集若具有相同的重要状态,且同时包含或同时不包含终态,则可看作等价
算法理解
下面这一篇文章对正则到DFA和DFA最小化的思想和具体实现剖析的比较透彻。其中正则到DFA并非重点考察内容,但对理解DFA优化的思想有比较大的帮助。
实例
最小化上面求得的DFA:

初始非终态{A, B, C, D},终态{E, F, G, H, I},
终态内部自己打转儿,不可再分
0将前者分裂为{A, B, C}和{D},1将前者分裂为{A, B}和{C},至此不可再分